18 Mar 2017

convolution neural network

目录

欢迎在文章下方评论，建议用电脑看

convolution neural network

深度学习可以说从2006年的泛起火花，在2012点开始爆发，而原因就是在ImageNet这个比赛上cnn的异常突出，在之后的好几年，冠军或者说前三基本上都是在cnn上做文章，有关cnn在ImageNet的论文很值得一读，我也大体看了下，并写了一篇笔记

卷积神经网络和上一章讲的常规神经网络非常相似：它们都是由神经元组成，神经元中有具有学习能力的权重和偏差。每个神经元都得到一些输入数据，进行内积运算后再进行激活函数运算。

四类解决方案解决图片的不变性（from PRML）

我们知道，在很多图片中，比如都存在一只猫，但那只猫的姿态或者形态是非常不同的，在我们人类看来这没什么，很容易知道它都是一只猫，但是，在计算机看来，就没有那么简单了，关于这种图片内容的不变性，我们可以有如下的方法来解决！

Data Augmentation：用神经网络生成多种变化

Tangent Propagation：用正则项的方式，用一个函数

Invariant feature：用一些特征用来做不变性

Neural Network structure with invariant properties (e.g. CNN)：用一些特征结构，比如cnn 开头

BackGround for cnn

  • 人眼在识别图像时，往往从局部到全局
  • 局部与局部之间联系往往不太紧密
  • 我们不需要神经网络中的每个结点都掌握全局的知识，因此可以从这里减少需要学习的参数数量

简介

  • 卷积神经网络主要由三种类型的层构成：卷积层，汇聚（Pooling）层和全连接层（全连接层和常规神经网络中的一样）。通过将这些层叠加起来，就可以构建一个完整的卷积神经网络。
  • 有的层有参数，有的没有（卷积层和全连接层有，ReLU层和汇聚层没有）。
  • 有的层有额外的超参数，有的没有（卷积层、全连接层和汇聚层有，ReLU层没有）。

下面是一个cnn神经网络结构的例子：

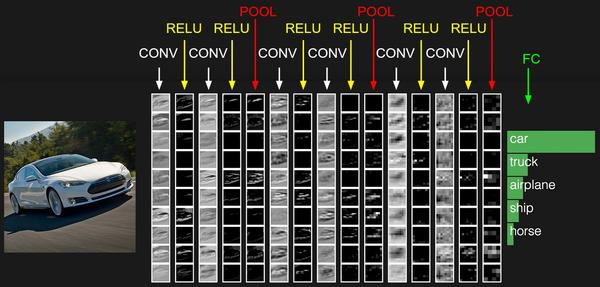
下面以层到层的顺序来讲解cnn：

卷积层

注意，一下讨论的前提是你熟悉了传统ANN的网络结构和一般知识，不明白的可以先看下我前面的博文，神经网络（基本概念），还有开头这篇神经网络-BP，更新参数策略

卷积计算

  • 其实，深度神经网络就是隐含层的数量较多，导致参数增多多，而我们可以理解卷积层存在的重要意义就是减少参数的数量。

  • 首先讨论的是，在没有大脑和生物意义上的神经元之类的比喻下，卷积层到底在计算什么。卷积层的参数是有一些可学习的滤波器集合构成的。每个滤波器(fiter)在空间上（宽度和高度）都比较小，但是深度和输入数据一致

  • 在深度一致的时候，n*n的fiter对m*m的图片做卷积运算的话，就会产生（m-n）/1+1（注意那个除以1是步长，在这里步长是1，当然也可以设置成其他的值，除不尽的情况是在外围加上几层，使得可以整除）的新的生成层，所以最重要的就是能整除

举个例子： 假设输入数据体尺寸为[32x32x3]（比如CIFAR-10的RGB图像），如果感受野（或滤波器尺寸）是5x5，那么卷积层中的每个神经元会有输入数据体中[5x5x3]区域的权重，共5x5x3=75个权重（还要加一个偏差参数）。注意这个连接在深度维度上的大小必须为3，和输入数据体的深度一致。但这样有什么用呢？请看下面：

局部链接

左图为全连接，右图为局部连接：

在上右图中，假如每个神经元只和10×10个像素值相连，那么权值数据为1000000×100个参数，减少为原来的万分之一。而那10×10个像素值对应的10×10个参数，其实就相当于卷积操作。所以，这样做的目的就是大大的减少了参数的数量。

参数共享

参数共享的原因:

如果在图像某些地方探测到一个水平的边界是很重要的，那么在其他一些地方也会同样是有用的，这是因为图像结构具有平移不变性。所以在卷积层的输出数据体的55x55个不同位置中，就没有必要重新学习去探测一个水平边界了。也就是说如果说一个卷积核在图片的一小块儿区域可以得到很好的特征，那么在其他的地方，也可以得到很好的特征。

理解图像的平移不变性，就是我们可以反过来看，把fiter的平移提取，看成是图片的相对平移，而用fiter去提取突出的特征。但需要注意的是，一个fiter就提取一种特征，所以会有下面的多卷积核

真实案例：Krizhevsky构架赢得了2012年的ImageNet挑战，其输入图像的尺寸是[227x227x3]。在第一个卷积层，神经元使用的感受野尺寸，步长，不使用零填充。因为(227-11)/4+1=55，卷积层的深度，则卷积层的输出数据体尺寸为[55x55x96]。55x55x96个神经元中，每个都和输入数据体中一个尺寸为[11x11x3]的区域全连接。在深度列上的96个神经元都是与输入数据体中同一个[11x11x3]区域连接，但是权重不同。有一个有趣的细节，在原论文中，说的输入图像尺寸是224x224，这是肯定错误的，因为(224-11)/4+1的结果不是整数。这件事在卷积神经网络的历史上让很多人迷惑，而这个错误到底是怎么发生的没人知道。我的猜测是Alex忘记在论文中指出自己使用了尺寸为3的额外的零填充。

  • 在卷积层中使用参数共享是用来控制参数的数量。就用上面的例子，在第一个卷积层就有55x55x96=290,400个神经元，每个有11x11x3=364个参数和1个偏差。将这些合起来就是290400x364=105,705,600个参数。单单第一层就有这么多参数，显然这个数目是非常大的。
  • 在一个深度切片中，每个滤波器都被55x55个神经元共享。注意参数共享的假设是有道理的：如果在图像某些地方探测到一个水平的边界是很重要的，那么在其他一些地方也会同样是有用的，这是因为图像结构具有平移不变性。共有96x11x11x3=34,848个不同的权重，或34,944个参数（+96个偏差）

相对全连接传统神经网络，ｃｎｎ的参数较少的原理就是参数共享和局部连接

注意:如果在一个深度切片中的所有权重都使用同一个权重向量，那么卷积层的前向传播在每个深度切片中可以看做是在计算神经元权重和输入数据体的卷积（这就是“卷积层”名字由来）。这也是为什么总是将这些权重集合称为滤波器（filter）（或卷积核（kernel）），因为它们和输入进行了卷积！

多卷积核

  • 可以认为多个卷积和就是在提取不同的方面的特征！
  • 上面所述只有100个参数时，表明只有1个10*10的卷积核，显然，特征提取是不充分的，我们可以添加多个卷积核，比如32个卷积核，可以学习32种特征。在有多个卷积核时，如下图所示：

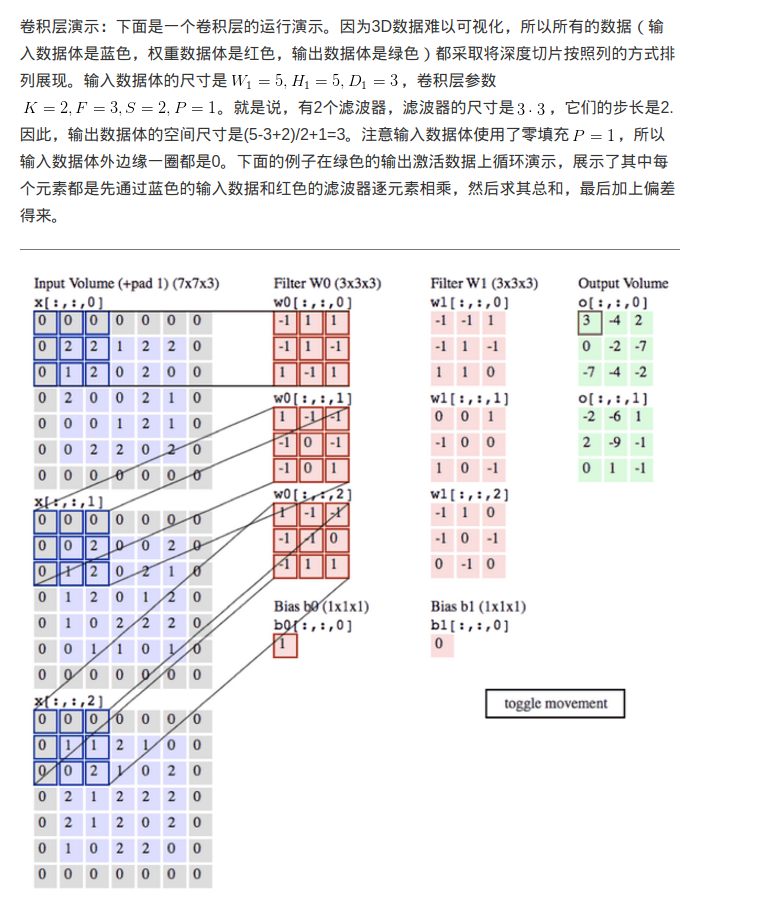
header1

注意，这里是只有两个filter，也就是说和深度无关，一个filter提取一种特征

关于卷积层的讲解，当然其他也讲的很好，大家可以看下cs231n课程中的笔记，特别是那个gif图片，讲两个卷积核详细的卷积运算过程，英文版;中文翻译

一些卷积层的trick&tip

如下：

1. 我们倾向于选择多层小size的卷积层，而不是一个大size的卷积层。

现在，我们以3个3x3的卷积层和1个7x7的卷积层为例，加以对比说明。从下图可以看出，这两种方法最终得到的activation map大小是一致的，但3个3x3的卷积层明显更好：

1)、3层的非线性组合要比1层线性组合提取出的特征具备更高的表达能力；
2)、3层小size的卷积层的参数数量要少，3x3x3<7x7；
3)、同样的，为了便于反向传播时的梯度计算，我们需要保留很多中间梯度，3层小size的卷积层需要保留的中间梯度更少。 ![](http://upload-images.jianshu.io/upload_images/2301760-f4dac7749cd64ada.png?imageMogr2/auto-orient/strip%7CimageView2/2/w/1240)

1×1的卷积大概有两个方面的作用

  1. 实现跨通道的交互和信息整合(NIN)
  2. 进行卷积核通道数的降维和升维(Residual network,google net)

这个详见ImageNet Evolution中的为什么可以是1×1卷积

汇聚层

  1. 在连续的卷积层之间会周期性地插入一个汇聚层。它的作用是逐渐降低数据体的空间尺寸，这样的话就能减少网络中参数的数量，使得计算资源耗费变少，也能有效控制过拟合，提取重要特征，符合不变性。汇聚层使用MAX操作，对输入数据体的每一个深度切片独立进行操作，改变它的空间尺寸。最常见的形式是汇聚层使用尺寸2x2的滤波器，以步长为2来对每个深度切片进行降采样，将其中75%的激活信息都丢掉。每个MAX操作是从4个数字中取最大值（也就是在深度切片中某个2x2的区域）。深度保持不变。
  2. 一般是2*2或者3*3，计算公式和卷积层的差不多
  3. 在池化单元内部能够具有平移的不变性，它的平移范围也是有一定范围的，因为每个池化单元都是连续的，所以能够保证图像整体上发生了平移一样能提取特征进行匹配。一般来说，都是用max或者是average，而max还是average都是在提取区域特征，均相当于一种抽象，抽象就是过滤掉了不必要的信息（当然也会损失信息细节），所以在抽象层次上可以进行更好的识别。至于max与average效果是否一样，还是要看需要识别的图像细节特征情况，这个不一定的，不过据说差异不会超过2%。

Max Pooling

在一个卷积层的输出层上取一个切片，取其中最大值代表这个切片

  • 优点
    • 不增加需要调整的参数
    • 通常比其他方法准确
  • 缺点：更多Hyper Parameter，包括要取最值的切片大小，以及去切片的步长

Average Pooling

在卷积层输出中，取切片，取平均值代表这个切片

有些人认为池化层并不是必要的，此外，有人发现去除池化层对于生成式模型（generative models）很重要，例如variational autoencoders(VAEs)，generative adversarial networks(GANs)。可能在以后的模型结构中，池化层会逐渐减少或者消失。

header1

归一化层

在卷积神经网络的结构中，提出了很多不同类型的归一化层，有时候是为了实现在生物大脑中观测到的抑制机制。比如在AlexNet 中的Local Response Nomalization ，但是这些层渐渐都不再流行，因为实践证明它们的效果即使存在，也是极其有限的。

当然，cnn中有很多都用到了batch normalization和dropout，关于这个trick的讲解，可以看下这篇博文

OutPut

将一个deep and narrow的feature层作为输入，传给一个Regular神经网络

Inception

对同一个卷积层输出，执行各种二次计算，将各种结果堆叠到新输出的depth方向上

这个在GoogLeNet中教具代表性，可以查看下

ＣＮＮ 的结构

最简单的CNNs结构的diagram（input+1conv+1pool+2fc）:

这里我们列举几种常见类型的卷积神经网络结构：

· INPUT --> FC/OUT      这其实就是个线性分类器
· INPUT --> CONV --> RELU --> FC/OUT
· INPUT --> [CONV --> RELU --> POOL]*2 --> FC --> RELU --> FC/OUT
· INPUT --> [CONV --> RELU --> CONV --> RELU --> POOL]*3 --> [FC --> RELU]*2 --> FC/OUT

最后，回到开头，强烈建议，关于几个重要的cnn的变形，大家可以看下那几篇在ImageNet的paper！

参考链接

Tags:
Stats:
comments


Share: