

现在,我们一起来了解下最近都大火的神经网络(neural network),它看起来,听起来很高大上,但是,事实上,理解起来也就这样啦,下面来一起看下吧!
以下大多笔记来自cs231n,一个非常不错的deep learning课,值得一看,奉上链接
注意:说神经网络多少层数的时候一般不包括输入层。 在神经网络中的激活主要讲的是梯度的更新的激活
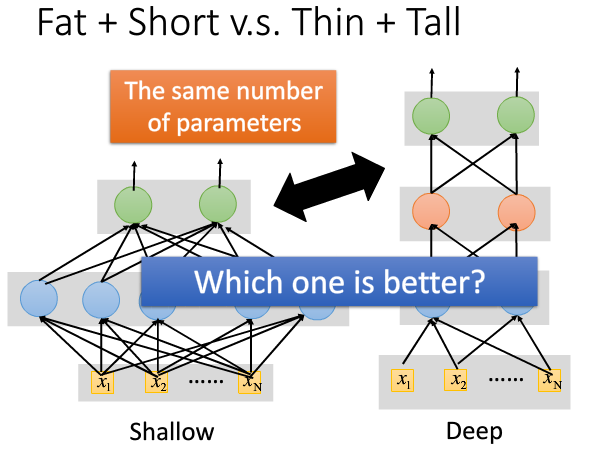
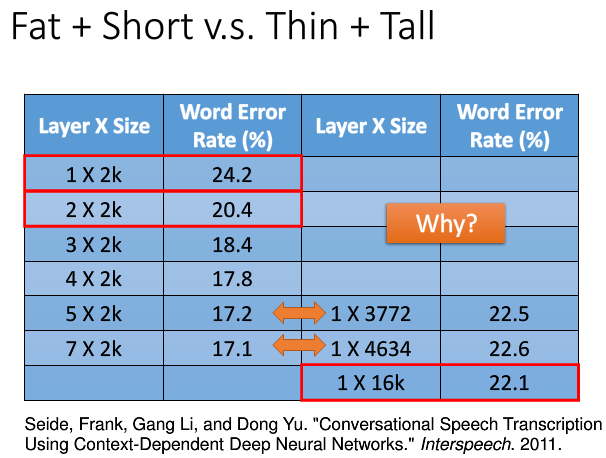
A shallow network has less number of hidden layers. While there are studies that a shallow network can fit any function, it will need to be really fat. That causes the number of parameters to increase a lot.
There are quite conclusive results that a deep network can fit functions better with less parameters than a shallow network.



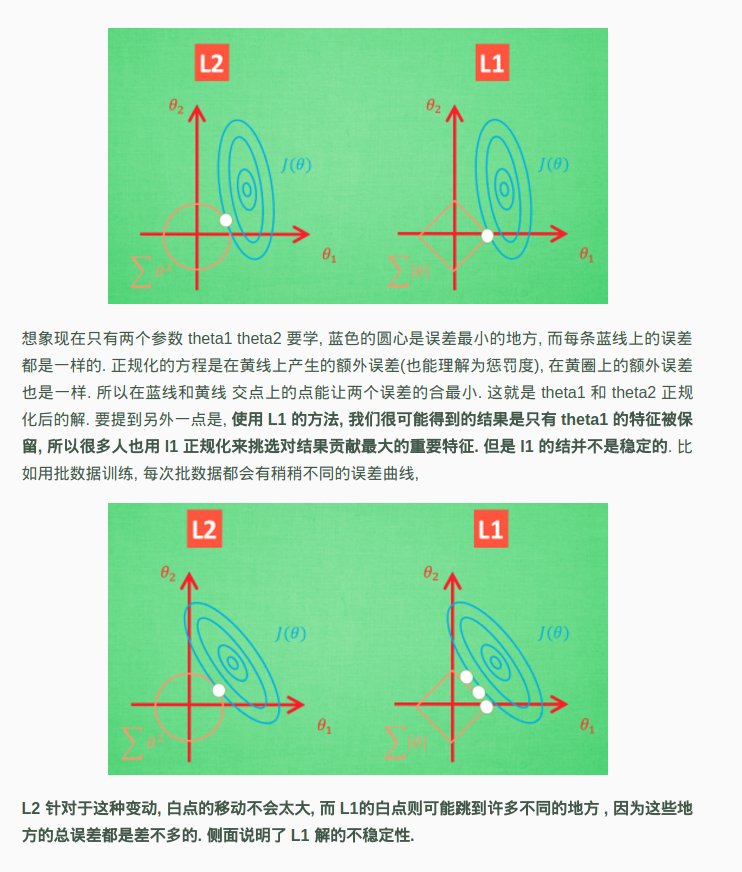
注意:L1正则化会让权重向量在最优化的过程中变得稀疏(即非常接近0);L2正则化可以直观理解为它对于大数值的权重向量进行严厉惩罚,倾向于更加分散的权重向量。
l1,l2正则化的图像化:
随机失活(Dropout):Dropout可以看作是Bagging的极限形式,每个模型都在当一情况中训练,同时模型的每个参数都经过与其他模型共享参数,从而高度正则化。在训练过程中,随机失活也可以被认为是对完整的神经网络抽样出一些子集,每次基于输入数据只更新子网络的参数(然而,数量巨大的子网络们并不是相互独立的,因为它们都共享参数)。在测试过程中不使用随机失活,可以理解为是对数量巨大的子网络们做了模型集成(model ensemble),以此来计算出一个平均的预测。关于这个,可以看下Batch-Normalization and dropout中的dropout部分
需要注意的是,在正则化的时候,bais是不需要正则化的,不然可能会导致欠拟合!具体看这篇博文
简单的从二维来理解,首先,图像数据是高度相关的,假设其分布如下图a所示(简化为2维)。由于初始化的时候,我们的参数一般都是0均值的,因此开始的拟合y=Wx+b,基本过原点附近(因为b接近于零),如图b红色虚线。因此,网络需要经过多次学习才能逐步达到如紫色实线的拟合,即收敛的比较慢。如果我们对输入数据先作减均值操作,如图c,显然可以加快学习。更进一步的,我们对数据再进行去相关操作,使得数据更加容易区分,这样又会加快训练,如图d。
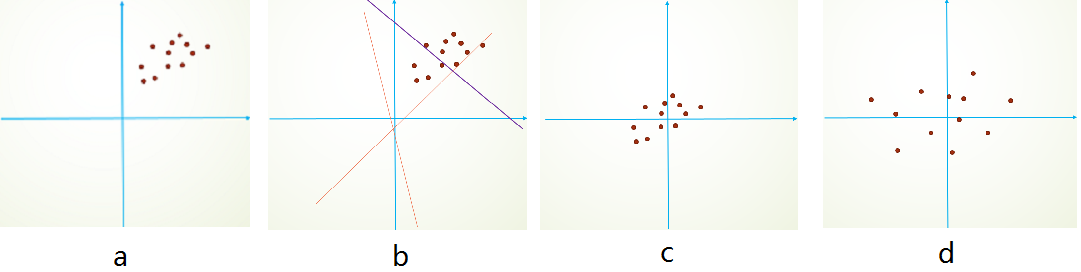
X /= np.std(X, axis=0)。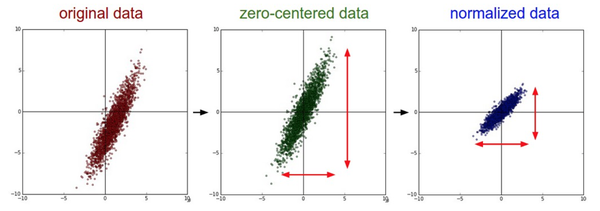
左边:原始的2维输入数据。中间:在每个维度上都减去平均值后得到零中心化数据,现在数据云是以原点为中心的。右边:每个维度都除以其标准差来调整其数值范围。红色的线指出了数据各维度的数值范围,在中间的零中心化数据的数值范围不同,但在右边归一化数据中数值范围相同。
PCA和白化(Whitening)是另一种预处理形式
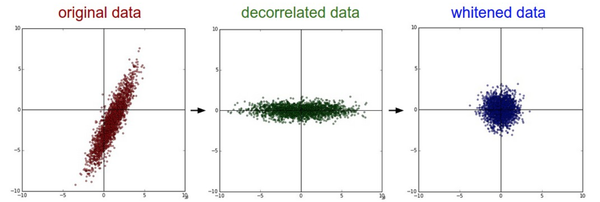
(中间是pca,右边是白化),
Batch Normalization就是在每一层的wx+b和f(wx+b)之间加一个归一化(将wx+b归一化成:均值为0,方差为1;但在原论文中,作者为了计算的稳定性,加了两个参数将数据又还原回去了,这两个参数也是需要训练的。)层,说白了,就是对每一层的数据都预处理一次。方便直观感受,上张图:
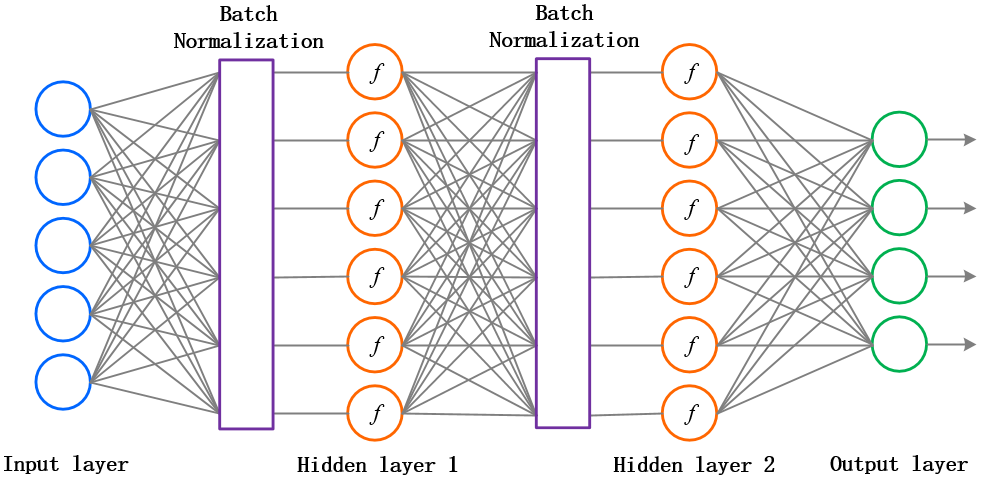
这个方法可以进一步加速收敛,因此学习率可以适当增大,加快训练速度;过拟合现象可以得倒一定程度的缓解,所以可以不用Dropout或用较低的Dropout,而且可以减小L2正则化系数,训练速度又再一次得到了提升。即Batch Normalization可以降低我们对正则化的依赖程度。
现在的深度神经网络基本都会用到Batch Normalization:其做法是让激活数据在训练开始前通过一个网络,网络处理数据使其服从标准高斯分布。在全连接之后做的操作
一句话总结:批量归一化可以理解为在网络的每一层之前都做预处理,只是这种操作以另一种方式与网络集成在了一起。搞定!
还有要注意的是,Batch Normalization和pca加白化有点类似,结果都是可以零均值加上单位方差,可以使得数据弱相关,但是在深度神经网络中,我们一般不要pca加白化,原因就是白化需要计算整个训练集的协方差矩阵、求逆等操作,计算量很大,此外,反向传播时,白化操作不一定可导。 最后,可以看下Batch-Normalization and dropout中的Batch-Normalization部分
下面是两个网上资料,关于为什么不能全零初始化:
小随机数初始化: 产生的数字为以零为平均值,单位标准差的高斯分布。使用这种方式,每个神经元的权重矩阵都从多维度高斯分布中随机初始化。所以神经元在输入空间内指向不同的方向。代码为w = np.random.randn(n) * sqrt(2.0/n)。这个形式是神经网络算法使用ReLU神经元时的当前最佳推荐。
稀疏初始化(Sparse initialization):每个神经元都同下一层固定数目的神经元随机连接(其权重数值由一个小的高斯分布生成)
偏置(biases)的初始化。通常将偏置初始化为0,这是因为随机小数值权重矩阵已经打破了对称性。对于ReLU非线性激活函数,有研究人员喜欢使用如0.01这样的小数值常量作为所有偏置的初始值,这是因为他们认为这样做能让所有的ReLU单元一开始就激活,这样就能保存并传播一些梯度。然而,这样做是不是总是能提高算法性能并不清楚(有时候实验结果反而显示性能更差),所以通常还是使用0来初始化偏置参数。
exp()在深度神经网络时候相比就比较慢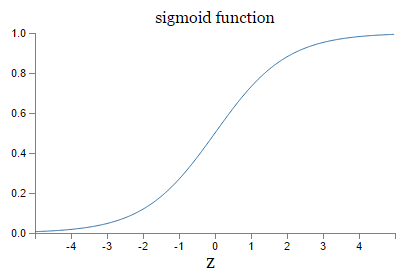
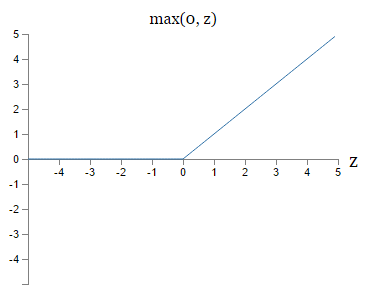
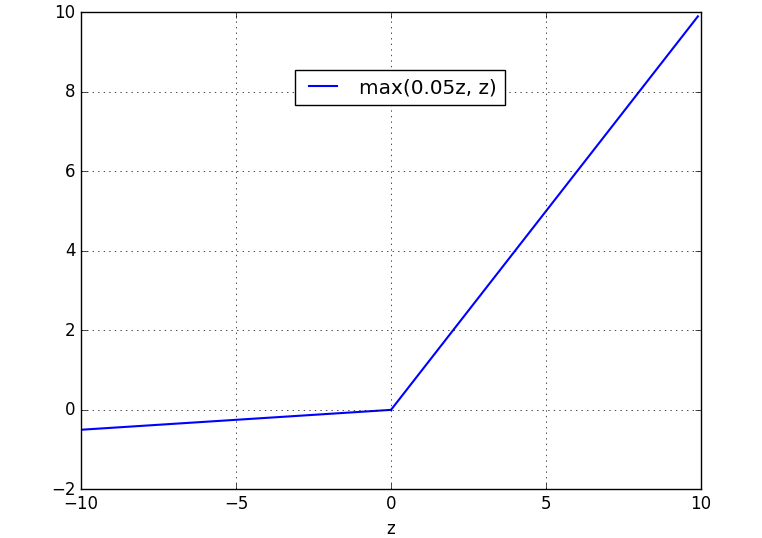
Kaiming He等人在2015年发布的论文Delving Deep into Rectifiers中介绍了一种新方法PReLU,把负区间上的斜率当做每个神经元中的一个参数。然而该激活函数在在不同任务中均有益处的一致性并没有特别清晰。
指数线性单元(Exponential Linear Units, ELU) ELU的公式为:
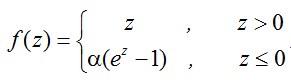
ELU.png 函数曲线如下:
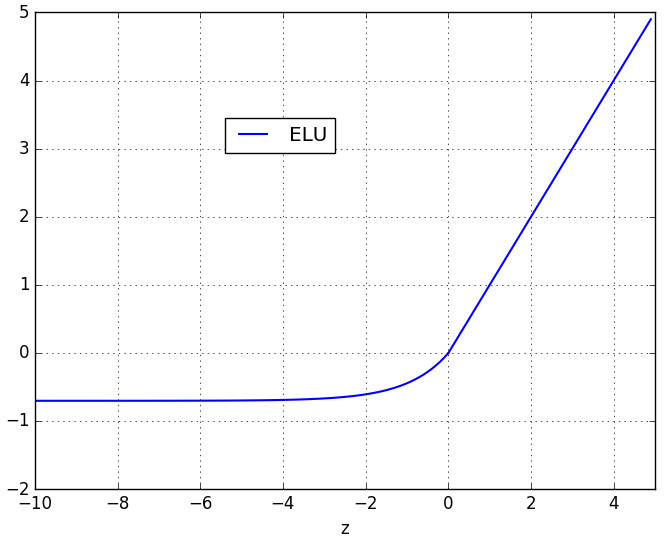
Maxout是对ReLU和leaky ReLU的一般化归纳
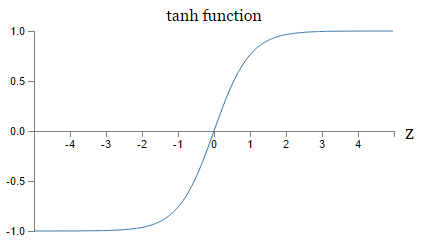
“那么该用那种呢?”用ReLU非线性函数。注意设置好学习率,(如果学习率设置得太高,可能会发现网络中40%的神经元都会死掉(在整个训练集中这些神经元都不会被激活)。通过合理设置学习率,这种情况的发生概率会降低。),解决方案:或许可以监控你的网络中死亡的神经元占的比例。如果单元死亡问题困扰你,就试试Leaky ReLU或者Maxout,不要再用sigmoid了。也可以试试tanh,但是其效果应该不如ReLU或者Maxout。
一个非常常见的,非常漂亮的成本函数是“交叉熵”(cross-entropy)。交叉熵产生于信息论里面的信息压缩编码技术,但是它后来演变成为从博弈论到机器学习等其他领域里的重要技术手段。它的定义如下:
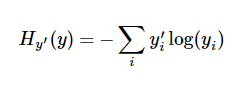
y 是我们预测的概率分布, y’ 是实际的分布(我们输入的one-hot vector)
交叉熵是正的,并且当所有输入x的输出都能接近期望输出y的话,交叉熵的值将会接近 0。这两个特征在直觉上我们都会觉得它适合做代价函数。事实上,我们的均方代价函数也同时满足这两个特征。这对于交叉熵来说是一个好消息。而且交叉熵有另一个均方代价函数不具备的特征,它能够避免学习速率降低的情况。
因为MSE(均方误差)不会出太大问题、同时也基本不能很好地解决问题,而折叶损失函数不能很好的描述概率和局部目标化(local objective)的问题,故一般都用这个交叉熵作为损失函数。
在现在的深度神经网络中,大多数情况下,我们使用的就是交叉熵这个代价函数 详细了解交叉熵