11 Feb 2017

模型选择与评价，降维

目录

欢迎在文章下方评论，建议用电脑看

模型指标

  1. 正确率 = 提取出的正确信息条数 / 提取出的信息条数
  2. 召回率 = 提取出的正确信息条数 / 样本中的信息条数

两者取值在0和1之间，数值越接近1，查准率或查全率就越高。

  1. F值 = 正确率 * 召回率 * 2 / (正确率 + 召回率) （F 值即为正确率和召回率的调和平均值）

不妨举这样一个例子：某池塘有1400条鲤鱼，300只虾，300只鳖。现在以捕鲤鱼为目的。撒一大网，逮着了700条鲤鱼，200只虾，100只鳖。那么，这些指标分别如下：

正确率 = 700 / (700 + 200 + 100) = 70%
召回率 = 700 / 1400 = 50%
F值 = 70% * 50% * 2 / (70% + 50%) = 58.3%

不妨看看如果把池子里的所有的鲤鱼、虾和鳖都一网打尽，这些指标又有何变化：

正确率 = 1400 / (1400 + 300 + 300) = 70%
-召回率 = 1400 / 1400 = 100%
F值 = 70% * 100% * 2 / (70% + 100%) = 82.35%

　　由此可见，正确率是评估捕获的成果中目标成果所占得比例；召回率，顾名思义，就是从关注领域中，召回目标类别的比例；而F值，则是综合这二者指标的评估指标，用于综合反映整体的指标。

评价分类器性能指标之AUC、ROC

引子

假设有下面两个分类器，哪个好？（样本中有A类样本90个，B 类样本10个。）

header1

分类器C1把所有的测试样本都分成了A类，分类器C2把A类的90个样本分对了70个，B类的10个样本分对了5个。

则C1的分类精度为 90%，C2的分类精度为75%，但直觉上，我们感觉C2更有用些。但是依照正确率来衡量的话，那么肯定C1的效果好一点。那么这和我们认为的是不一致的。也就是说，有些时候，仅仅依靠正确率是不妥当的。

我们还需要一个评价指标，能客观反映对正样本、负样本综合预测的能力，还要考虑消除样本倾斜的影响（其实就是归一化之类的思想，实际中很重要，比如pv总是远远大于click），这就是auc指标能解决的问题。

ROC

为了理解auc，我们需要先来弄懂ROC。 先来看一个普遍的二分类问题的结果，预测值和实际值有4种组合情况，看下面的表格：

注意这里就只有两个分类，所以FN就表示的是分错的pos类，同理FP就表示的是分错的neg类

我们定义一个变量：

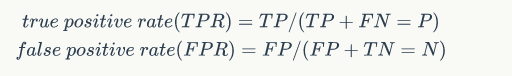
header1

看图也就可以知道：

  1. TPR表示的就是预测正确且实际分类为正的数量 与 所有正样本的数量的比例。–实际的正样本中，正确预测的比例是多少？
  2. FPR表示的是预测错误且实际分类为负的数量 与所有负样本数量的比例。 –实际的负样本当中，错误预测的比例是多少？

下面来看一则对话来理解recell，accuracy和precison：

What percent of your predictions were correct?
You answer: the "accuracy" was (TP+TN)/ALL
What percent of the positive cases did you catch?
You answer: the "recall" TP/(TP+FN)
What percent of positive predictions were correct?
You answer: the "precision" was TP/(TP+FP)

可以代入到上面的两个分类器当中，可以得到下面的表格（分类器C1）：

header1

TPR = FPR = 1.0

分类器C2：

header1

TPR = 0.78， FPR = 0.5

那么，以TPR为纵坐标，FPR为横坐标画图，可以得到：

上图中蓝色表示C1分类器，绿色表示C2分类器。可以知道，这个时候绿色的点比较靠近左上角，可以看做是分类效果较好。所以评估标准改为离左上角近的是好的分类器（考虑了正负样本的综合分类能力）。

一连串这样的点构成了一条曲线，该曲线就是ROC曲线。而ROC曲线下的面积就是AUC（Area under the curve of ROC）。这就是AUC指标的由来。

如何画ROC曲线

对于一个特定的分类器和测试数据集，显然只能得到一个分类结果，即一组FPR和TPR结果，而要得到一个曲线，我们实际上需要一系列FPR和TPR的值才能得到这样的曲线，这又是如何得到的呢？

可以通过分类器的一个重要功能“概率输出”，即表示分类器认为某个样本具有多大的概率属于正样本（或负样本），来动态调整一个样本是否属于正负样本（还记得当时阿里比赛的时候有一个表示被判定为正样本的概率的列么？）

假如我们已经得到了所有样本的概率输出（属于正样本的概率），现在的问题是如何改变这个阈值（概率输出）？我们根据每个测试样本属于正样本的概率值从大到小排序。下图是一个示例，图中共有20个测试样本，“Class”一栏表示每个测试样本真正的标签（p表示正样本，n表示负样本），“Score”表示每个测试样本属于正样本的概率。

接下来，我们从高到低，依次将“Score”值作为阈值，当测试样本属于正样本的概率大于或等于这个阈值时，我们认为它为正样本，否则为负样本。举例来说，对于图中的第4个样本，其“Score”值为0.6，那么样本1，2，3，4都被认为是正样本，因为它们的“Score”值都大于等于0.6，而其他样本则都认为是负样本。每次选取一个不同的阈值，我们就可以得到一组FPR和TPR，即ROC曲线上的一点。这样一来，我们一共得到了20组FPR和TPR的值，将它们画在ROC曲线的结果如下图：

当我们将阈值设置为1和0时，分别可以得到ROC曲线上的(0,0)和(1,1)两个点。将这些(FPR,TPR)对连接起来，就得到了ROC曲线。当阈值取值越多，ROC曲线越平滑。

–在阿里比赛的时候还以为ROC是没用的！！！真的是有眼无珠啊！！！还是有疑惑的是：如何根据ROC来判定结果的好换呢？看哪个分类器更加接近左上角吧。同时，可以根据ROC来确定划定正样本的概率边界选择在哪里比较合适！！！原来是这样！！！

AUC值的计算

AUC（Area Under Curve）被定义为ROC曲线下的面积，显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方，所以AUC的取值范围在0.5和1之间。使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好，而作为一个数值，对应AUC更大的分类器效果更好。

为什么使用ROC

既然已经这么多评价标准，为什么还要使用ROC和AUC呢？因为ROC曲线有个很好的特性：当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡（class imbalance）现象，即负样本比正样本多很多（或者相反），而且测试数据中的正负样本的分布也可能随着时间变化。下图是ROC曲线和Precision-Recall曲线的对比：

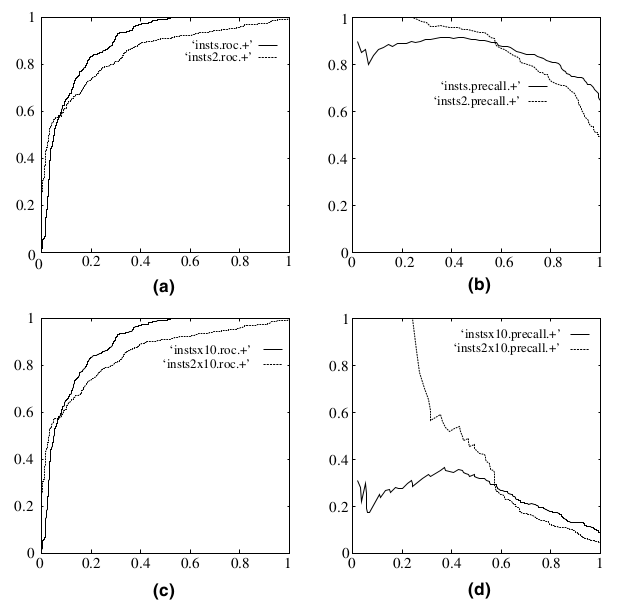
在上图中，(a)和(c)为ROC曲线，(b)和(d)为Precision-Recall曲线。(a)和(b)展示的是分类其在原始测试集（正负样本分布平衡）的结果，(c)和(d)是将测试集中负样本的数量增加到原来的10倍后，分类器的结果。可以明显的看出，ROC曲线基本保持原貌，而Precision-Recall曲线则变化较大。

降维技术

  • 在我们解决机器学习的问题时,常常要从维度上做文章。有时候我们需要增维, 比如 kernel methods 就可以在高纬度上重构样本从而解决样本在低维上不的线性不可分问题(高斯 kernel 甚至可以把样本在无穷维上展开)。有时候我们又需要降维,因为我们是三维生物,我们最多只能理解三维世界, 所以想要看看手头的数据, 就必须把它们降到三维以内; 另外,往往很多特征没什么用处, 我们可以可以通过降维或者特征工程的手段来把它们剔除,降低计算复杂度。
  • 在这篇文章中，我主要讲解PCA，Factor Analysis，和Independent Component Analysis。

PCA

PCA预处理

  • PCA算法，不过通常在PCA算法运行前，我们需要对数据进行预处理——对数据的期望及方差进行标准化
  1. 整体的数据的期望设为0
  2. 各个分量用统一的标准定义，（如一个人的身高，体重…）

注意，这PCA将白了就是线代中特征分解的应用，所以特征分解要懂，了解可以看下这篇博文特征分解

PCA算法

  • PCA 希望可以找到那 些最重要的维度(假设 k 个重要维度,k<m),然后把 X 映射到这些重要维度上,用这 k 个映射系数作为新的 feature 于是样本们就被降低到了 k 维上。
  • 假设我们有 N 个样本,每个为 m 维,即 ,怎样定义重要维度呢?假设 u(一个 m 维向量)是一个重要维度,令 u 把 X 射成 这样的 N 个点,u 之所以重要,因为新生成的 N 个点的方差是最大的,于是样本间的差异性就被保存了下来, 我们还是可以在新的样本空间里做聚类,分类等操作。所以 PCA 背后的优化问题其实是,

所以 PCA 的一般步骤是:

  1. 将数据正规化为零期望以及单位化方差；
  2. 对样本数据的协方差矩阵(covariance matrix)做计算，得到特征值
  3. 特征值 (eigen values) 排序
  4. top­k 特征值对应的特征向量 (eigen vectors) 找出来
  5. 把 X 映射到这 k 个特征向量上

SVD（奇异值分解）

  • 他是另一种实现PCA的另一种说法
  • 可以将数据映射到低维空间，常用于从有噪声数据中抽取相关特征。
  • 详细讲解可以看另一个博文：奇异值分解
  • 特征分解和奇异值分解：不是所有的矩阵都能对角化（对称矩阵总是可以），而所有矩阵总是可以做奇异值分解的。所以因为这个，导致的是在PCA中，他们两者的是一样的（在这里就是同一个东西），因为协方差矩阵是对称的，然后再其他方面，SVD有更加广泛的应用，比如：在推荐算法方面，可以使得数据集更易使用，简单计算，这个详见《机器学习实战》中SVD分解那一章

举例：

注意一开始的数据是三维的：

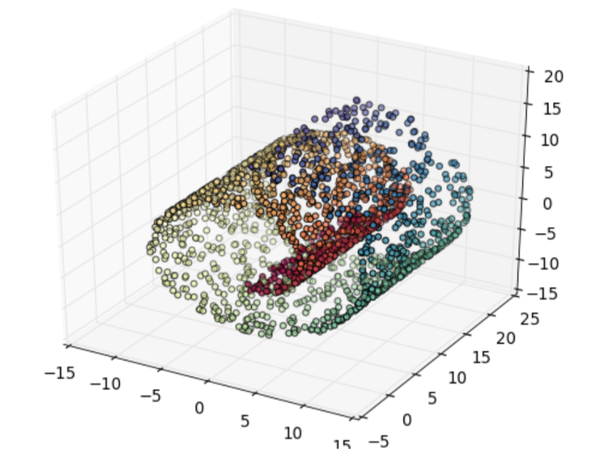
经过PCA之后的图：

Factor Analysis（因子分析）

Factor Analysis: FA 的思想与 PCA 其实很相似,假设高维度上的观测结果 X 其实是由低维 度上的 factors 来支配的。打个比方,笔者身边有一大群妹子,每个妹子都有很多的参数,例 如,身高,体重,肺活量,皮肤,眼睛大小,脸蛋形状,发型,性格等 8 个参数… 笔者经过大 量的调查研究把每个妹子在每个 feature 上都打了从 1­到10 的分数(10 分最高),然后就在纠 结,到底要对哪个下手呢?于是就想把妹子们做个 ranking,但是只能 rank 一维的数据呀,于 是就在想能不能把妹子的 8 个 feature 抽象成一个终极打分 ­­ 美貌。于是做了如下的假设:

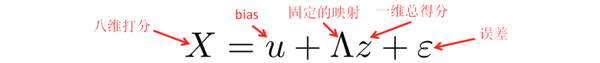
假设每个妹子都有一个终极打分 z(一维),这个分数将会通过一个固定的映射到八个维度 上,然后加上 bias 修正,再加上一些误差(误差保证尽管俩妹子得分一样,也可以春兰秋菊 各有千秋),于是就得到了八维打分 X。这个过程的原理可以让下面这俩图来解释一下: 首先强行把一维的数据搬到二维平面的一条直线上,再加上噪声,bias,于是就 得到了红圈里的一个二维的数据,把二维想象成八维就重构了妹子们的参数。

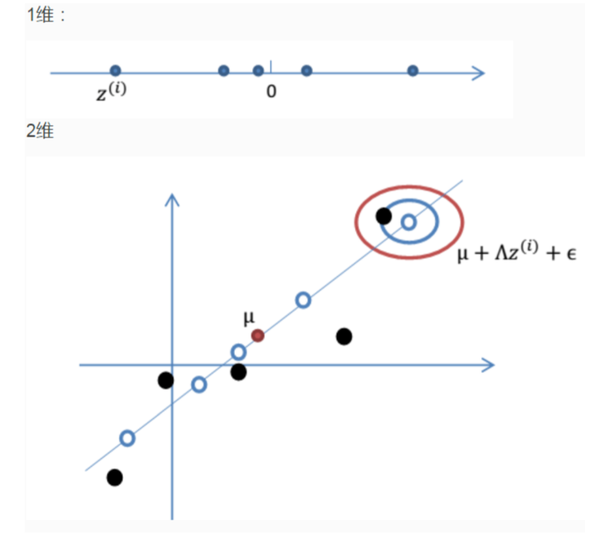
有了这个模型,我们就可以就用 EM(expectation­maxminization) 来估算 , 估算过程比较复杂,一句话讲就是通过调整这些参数,令 P(X) 出现的概率最大。 模型确定下来,就可以算出妹子们的最终得分 z, 排个序, 就可以从容地选择了! 继续看下蛋卷图

上面比较简略的讲述了一下因子分析，下面再通过一个简单例子，来表述因子分析背后的思想。

假设我们有m=5个2维的样本点x(i)（两个特征），如下：

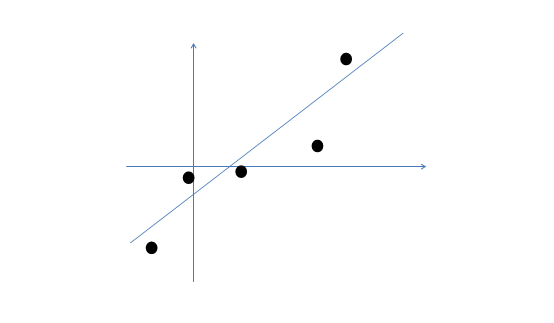
那么按照因子分析的理解，样本点的生成过程如下：

1、 我们首先认为在1维空间（这里k=1），存在着按正态分布生成的m个点z(i)，如下

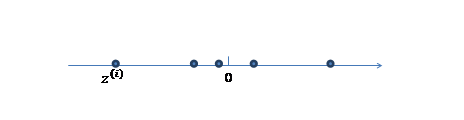
均值为0，方差为1。

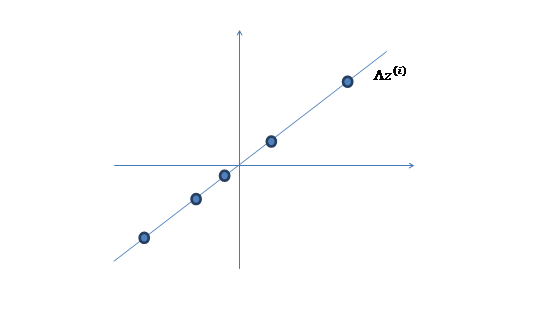
2、 然后使用某个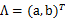将一维的z映射到2维，图形表示如下：

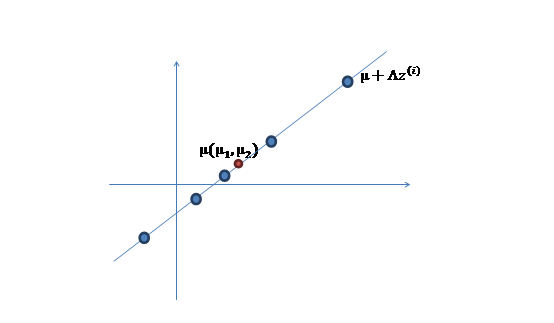
3、 之后加上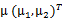，即将所有点的横坐标移动u1，纵坐标移动u2，将直线移到一个位置，使得直线过点u，原始左边轴的原点现在为u（红色点）。

然而，样本点不可能这么规则，在模型上会有一定偏差，因此我们需要将上步生成的点做一些扰动（误差），扰动。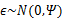

4、 加入扰动后，我们得到黑色样本x(i)如下：

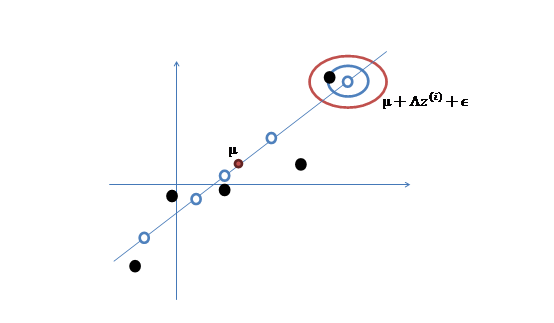
5、 其中由于z和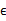的均值都为0，因此u也是原始样本点（黑色点）的均值。

由以上的直观分析，我们知道了因子分析其实就是认为高维样本点实际上是由低维样本点经过高斯分布、线性变换、误差扰动生成的，因此高维数据可以使用低维来表示。

在我们这篇博文中，我们只讲了降维方面，其实因子分析也是一个模型，但在这里不讲了，推荐一篇博文，有兴趣可以看下：因子分析

ICA（独立成分分析）

PCA是一种数据降维的方法，但是只对符合高斯分布的样本点比较有效，那么对于其他分布的样本，有没有主元分解的方法呢？来，下面我们来讲一个叫做独自成分分析的降维方式！

鸡尾酒宴会问题

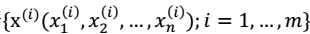  • n个人，n个麦克风。从n个麦克风得到一组数据：。其中：i 表示采样的时间顺序，也就是说共得到了 m 组采样，每一组采样都是 n 维的。
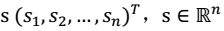  • 我们的目标是单单从这 m 组采样数据中分辨出每个人说话的信号s。有 n 个信号源 ，,s相互独立。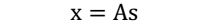
  • A 是一个未知的混合矩阵（mixing matrix），用来组合叠加信号 s。
  1. 我们可以得到：

    其中， x 不是一个向量，是一个矩阵

  2. 其中每个列向量

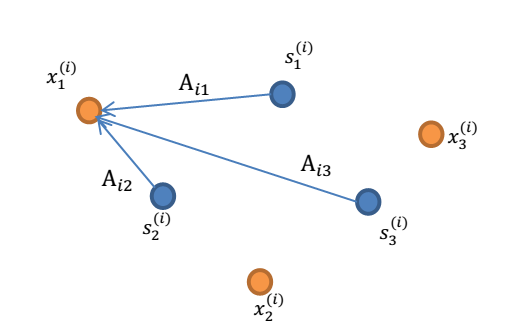
  3. A 和 s 都是未知的，x 是已知的，我们要想办法根据 x 来推出 s。这个过程也称作为盲信号分离。

  4. 最终得到：

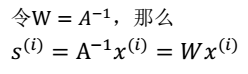
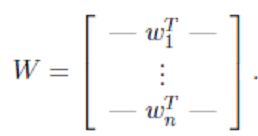
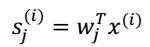
$s_{(i)}^{j}$：表示speaker j 在时刻i发出的信号。 对于此，我们需要知道两个量才能求出另外一个，下面我们进一步分析。

ICA算法的前处理步骤

  1. 中心化：也就是求 x 均值，然后让所有 x 减去均值，这一步与 PCA 一致。
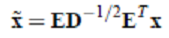  2. 漂白：目的是为了让x相互独立。将 x 乘以一个矩阵变成 (其协方差矩阵是$I$)。 其中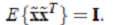， 其中使用特征值分解来得到 E（特征向量矩阵）和 D（特征值对角矩阵） ，计算公式为

ICA算法

  1. 我们假定每$s_i$有概率密度$p_s$，那么给定时刻原信号的联合分布就是

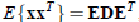
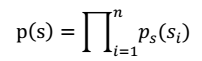
    注：每个人发出的声音信号s各自独立。

  2. 然后，我们就可以求得p(x)

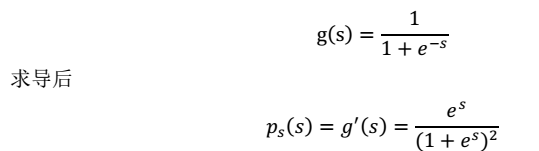
  3. 现在，我们需要知道p(s)和w，才能求得p(x)。 首先，我们假设s 的累积分布函数符合 sigmoid 函数

这就是 s 的密度函数。这里 s 是实数。

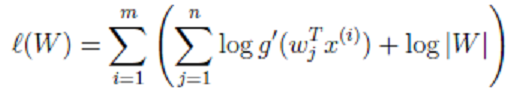
  1. 然后，我们就剩下W了。我们用最大似然估计的方法求解。 使用前面得到的 x 的概率密度函数，得

最终，我们求得：

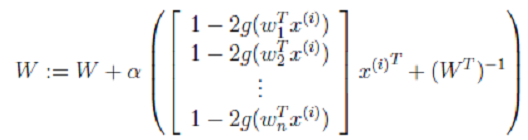
其中α是梯度上升速率，人为指定。

  1. 迭代求出 W 后，我们也可以还原出原始信号：

IAC应用

如果把麦克风x换成采集脑电波的电极，信号源s就代表大脑独立进程：心跳、眨眼等。通过将信号x减去心跳、眨眼等无用信号，我们就可以得到大脑内部信号。

小结

  • ICA 的盲信号分析领域的一个强有力方法，也是求非高斯分布数据隐含因子的方法。
  • ICA和PCA对比：

ICA: 从之前我们熟悉的样本-特征角度看，我们使用 ICA 的前提条件是，认为样本数据由独立非高斯分布的隐含因子产生，隐含因子个数等于特征数。更适合用来还原信号（因为信号比较有规律，经常不是高斯分布的）。 PCA : 认为特征是由 k 个正交的特征（也可看作是隐含因子）生成的。更适合用来降维（用那么多特征干嘛，k 个正交的即可） 有时候也需要组合两者一起使用。

最后：在这篇博文笔记中，我们学习了一些特征工程的方法，AOC和AUC，还有一些具体的降维技术，这些都是比较基础的，还有很多没有讲到的，现在先不讲了把，以后有机会再说（逃）

参考资料：

《统计学习方法》-李航
《机器学习》-周志华
《机器学习实战》-Peter Harrington
斯坦福大学公开课-机器学习
网上的各位大牛的博文

Tags:
Stats:
comments


Share: