欢迎在文章下方评论，建议用电脑看
最简单的一种机器学习模型，这个其实在高中（还是初中？）的时候我们就已经学过了，只不过那个时候觉的没什么用，也就大多数还给老师了！ 先来一个例子，来来简单的说说它！ 假设我们有一个经调查得到的数据集，内容是关于俄勒冈州波特兰地区47间出租公寓的面积与价格之间的关系表：
有了这样的数据，我们怎样才能预测波特兰地区其他出租公寓的价格，比如推如果一开始选的点就是最低点，那随机梯度下降将会怎么工作 答：会保持选的点就是最佳参数，这是因为那个偏导数为0（联系2次函数） 导出一个从面积得出价格的函数。这就转化为一个回归的问题：利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。
通俗的说就是，给定一定量的现有数据，用这些数据来拟合出一个函数，然后对新的数据进行拟合，就可以得出一个函数值，这个值就作为预测值。
下面我们结合上面的例子，先画出其数据的点
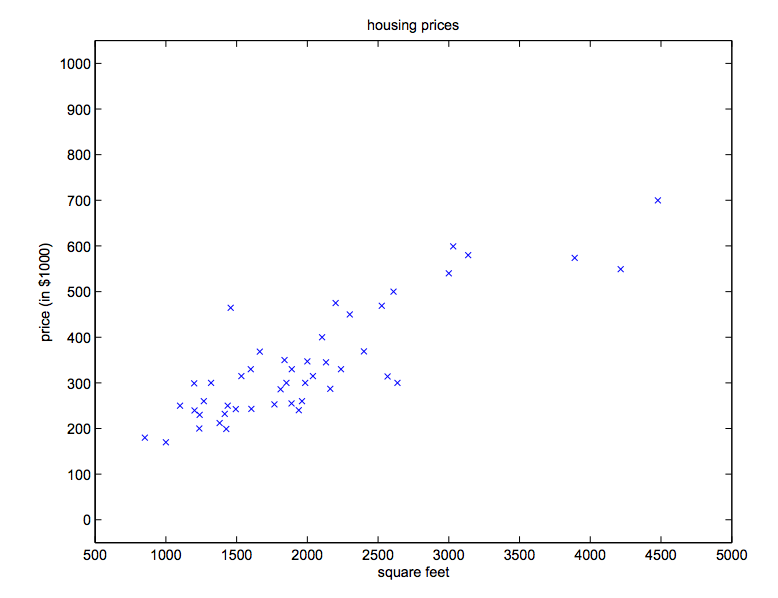
然后我们用这些数据来拟合一条直线，然后如果给我们一个新的数据，只知道他多少平方米，这个时候我们代入那个函数h（x）=θ*x+b(θ，b是参数，x是自变量)，得到预测值，就可以作为这个房子的预测价格了！（线性回归就是这样，看！多简单是吧！）
当然，整体上很简单，但细节我们还是要抠的，下面我们讲下细节和他的推广！
上面我们讨论了单个属性的回归，现在我们来讨论多个属性（n个）属性的回归。 下面给出公式：
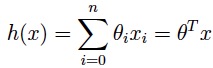
其实也是同样简单，我们只需要按照最简单的1个属性那样理解它就可以了，反正我是这样干的！现在有了目标函数，我们的目标是找到能预测最准的函数，那该怎么找能，就引出下下文：
我们这样想，有了上面的目标函数，我们最关键的是求出那些参数是吧，那现在我们能不能转变一个方向，看看从另一个方式，得到那些最优的参数，先看个式子：
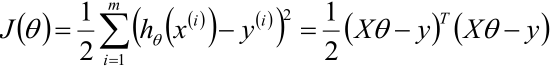
这个叫成本函数，具体其他成本函数讲解可以看我的上一篇博文,好了，为什么，肯定很多人跟我一样，一眼看到这个式子的就想问为什么？为什么是平方差？为什么是误差平方和而不是绝对值或其他损失函数？为什么前面要加个1/2？下面一个一个解释:
首先解释一下，上面那个成本函数是最小二乘回归模型中常见的最小二乘成本函数,最小二乘又是什么？
最小二乘（LS）问题是这样一类优化问题，目标函数是若干项的平方和，每一项具有形式，具体形式如下：
或者如下：
其中y是真值，
是估计值，式1和式2是一样的，只是用的符号不同，式1中的x对应式2中的θ ，即优化中要求的变量。
说下为什么在这里我们要为前面添加一个1/2，因为在之后的求导中能更简单的化简而且不会对结果产生影响！
最小二乘法的二乘是什么:简单地说,最小二乘的思想就是要使得观测点和估计点的距离的平方和达到最小.这里的“二乘”指的是用平方来度量观测点与估计点的远近（在古汉语中“平方”称为“二乘”）,“最小”指的是参数的估计值要保证各个观测点与估计点的距离的平方和达到最小.. 为什么要二乘:因为观测点和估计点之差可正可负,简单求和可能将很大的误差抵消掉,只有平方和才能反映二者在总体上的接近程度.
为什么使用最小二乘成本函数J？这样合理吗？有那么多别的指标，比如预测值与实际值之差的绝对值、四次方等，为什么偏偏选择差的平方作为优化指标？我们将从一系列基于概率的假设中推出最小二乘回归的合理性。
首先我们得复习一下线性回归的模型及假设：
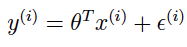
ε(i) ∼ N(0, σ2)，随机误差ε服从正态分布（高斯分布） ε(i) are distributed IID，随机误差ε是独立同分布的 于是可以获得目标变量的条件概率分布：
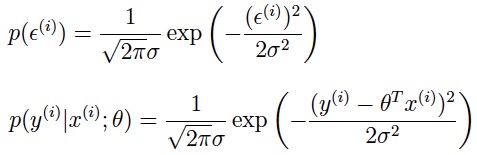
整个训练集的似然函数，与对数似然函数分别为：
因此，最大化对数似然函数，也就相当于最小化,于是，我们发现，圈着的这个式子正是成本函数J(θ)的定义式。
综上，可以看出，在关于训练数据的概率假设中，最小二乘回归与θθ的最大似然估计一致。也正是因为最小二乘回归其实是再做最大似然估计，所以我们才会强调最小二乘是一种“很自然”的方法。（不过，概率假设并不是证明“最小二乘是一种非常易用的、合理的求解过程”这一结论的必要条件，这只是众多假设中的一种，最小二乘在这种假设下合理，除此之外还有其他假设也可以证明这一结论。）
有了成本函数，我们下一步自然要求解最小的成本函数，找到最优的参数，所以这里就转变成为了求最小值的问题。在这里我就介绍两种方法吧，至于牛顿法，拟牛顿法，坐标法和他们的推广就下次再讲吧！
这个很简单。就是我们平时学的求解一个函数的通用方法，直接求导，然后使得导数等于0，求得驻点，最后得到最小值！对于上面的成本函数的求解如下：
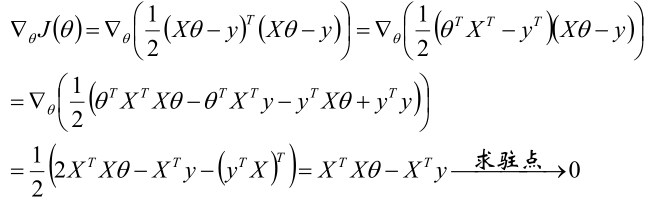
得到结果是：
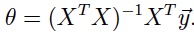
中间的求解过程有点点复杂。我们主要要记住那个结论的式子。然后改怎么记呢？这里给出一个小小的tips（我也是网上看到的），这个结果有个简单的记法(可以这样记，但一旦有人问这个结果的来历，可不能这样回答)：Xθ= y => X^TXθ= X^Ty => θ= (X^T X)^ -1*X^Ty
讲到正规方程组，然后再讲讲伪拟和岭回归!
什么是广义逆矩阵，请看下图：
介绍完上面的正规方程组，下面来看下另一种比较简单的优化算法–梯度下降，这个算法很重要，在机器学习领域，很多地方都用到，包括那些现在比较火的深度神经网络的求解！
首先看下式子：
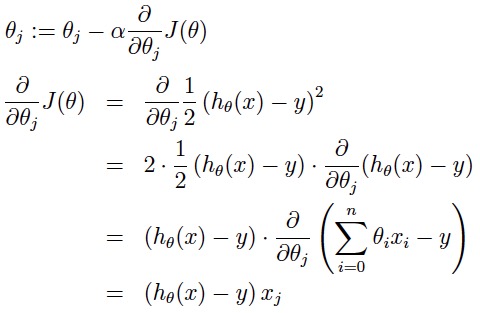[a表示的是步长或者说是学习率（learning rate）]
好了，怎么理解？在直观上，我们可以这样理解，看下图，一开始的时候我们随机站在一个点，把他看成一座山，每一步，我们都以下降最多的路线来下山，那么，在这个过程中我们到达山底（最优点）是最快的，而上面的a，它决定了我们“向下山走”时每一步的大小，过小的话收敛太慢，过大的话可能错过最小值）。这是一种很自然的算法，每一步总是寻找使J下降最“陡”的方向（就像找最快下山的路一样）。
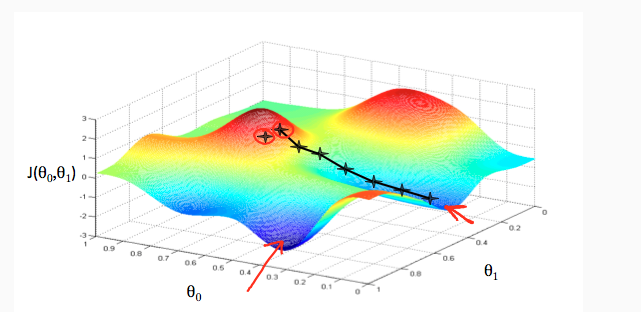
当然了，我们直观上理解了之后，接下来肯定是从数学的角度，我们可以这样想，先想在低维的时候，比如二维，我们要找到最小值，其实可以是这样的方法，具体化到1元函数中时，梯度方向首先是沿着曲线的切线的，然后取切线向上增长的方向为梯度方向，2元或者多元函数中，梯度向量为函数值f对每个变量的导数，该向量的方向就是梯度的方向，当然向量的大小也就是梯度的大小。现在假设我们要求函数的最值，采用梯度下降法，结合如图所示：
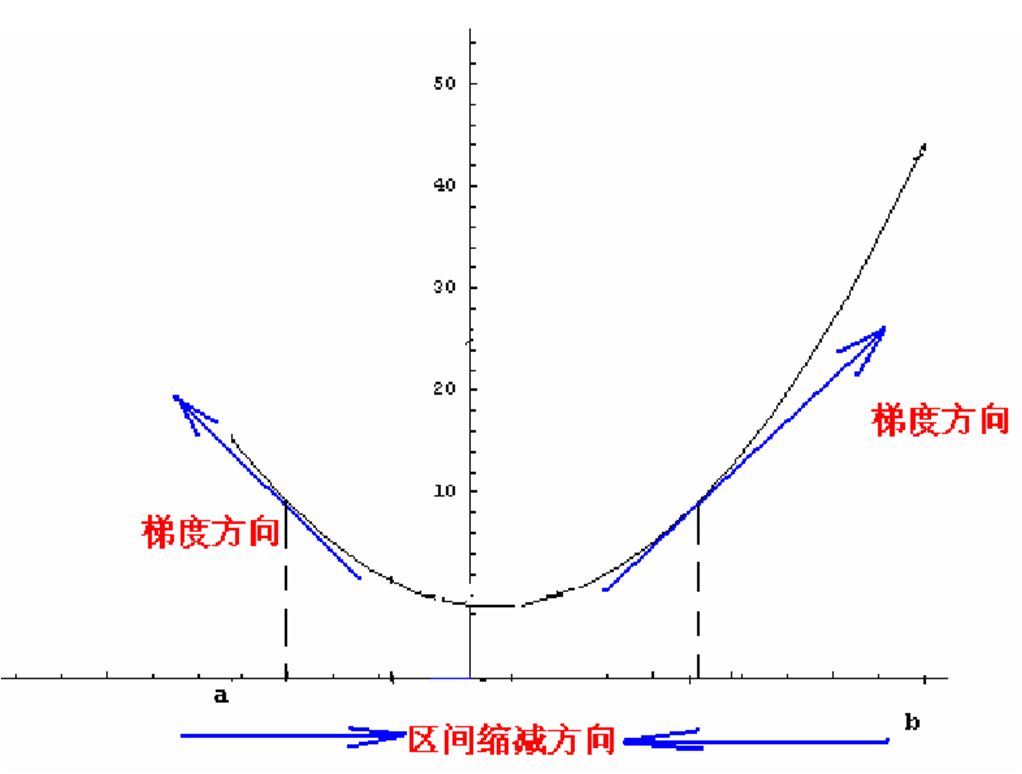
如图所示，我们假设函数是y=x^2+1,那么如何使得这个函数达到最小值呢，简单的理解，就是对x求导，得到y‘=1/2*x，然后有梯度下降的方式，如果初始值是（0的左边）负值,那么这是导数也是负值，用梯度下降的公式，使得x更加的靠近0,如果是正值的时候同理！
下面是两种梯度下降的方式:
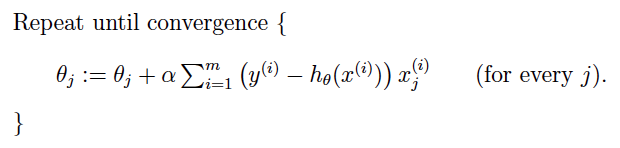
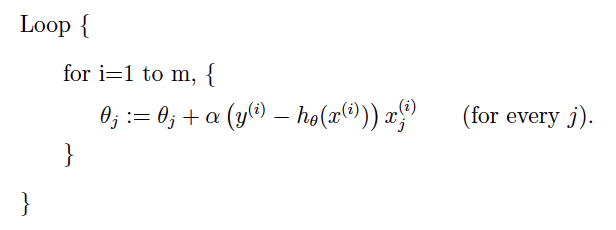
问1：如果一开始选的点就是最低点，那随机梯度下降将会怎么工作
答1：会保持选的点就是最佳参数，这是因为那个偏导数为0（联系2次函数）
问2：梯度下降的公式是怎么来的
答2：理解在2次函数的时候来理解，就是参数减去导数的值，然后更新参数，来自：coursera机器学习
问3：批量和随机梯度的本质区别是什么
答4：就是成本函数的不同，批量是计算把所有的数据都误差和，然后求导得，随机的成本函数是随机拿一条数据来作为误差，然后求导
首先在局部加权回归中，上面的损失函数变为
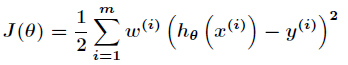
其中:
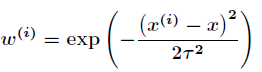
函数中的τ称作带宽（bandwidth）（或波长）参数，它控制了权值随距离下降的速率。如果τ取值较小，则会得到一个较窄的钟形曲线，这意味着离给定查询点x较远的训练样本x(i)的权值（对查询点xx附近训练样本的拟合的影响）将下降的非常快；而τ较大时，则会得到一个较为平缓的曲线，于是查询点附近的训练样本的权重随距离而下降的速度就会相对比较慢。
若直接求解得到最终的参数求解式子是：
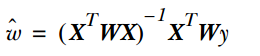
下面从图来直观感受局部加权回归和普通回归的不同：
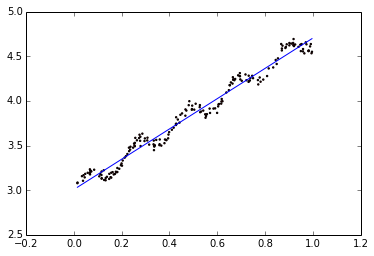
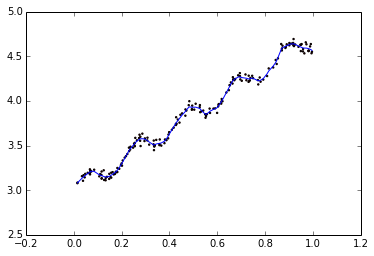
自变量是多个标量，或者理解成一个多维的向量。那么，函数随自变量的变化怎么刻画呢？一个方法，就是衡量函数在给定方向上的变化率，这就是方向导数。方向导数的特例，就是函数随各个自变量（标量）的变化率，即函数的偏导数，也就是函数沿各个坐标轴正方向的方向导数。
看高数下册 详数学推导 最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。
参考资料：
《统计学习方法》-李航
《机器学习》-周志华
《机器学习实战》-Peter Harrington
斯坦福大学公开课-机器学习
网上的各位大牛的博文
