

欢迎在文章下方评论,建议用电脑看
因为一个老是说概念可能会不那么清晰,在这篇文章中有例子详解推荐系统例子
还有这篇博文特征工程怎么做也值得借鉴
下面直接上图,在大体上对特征工程有个大概了解!
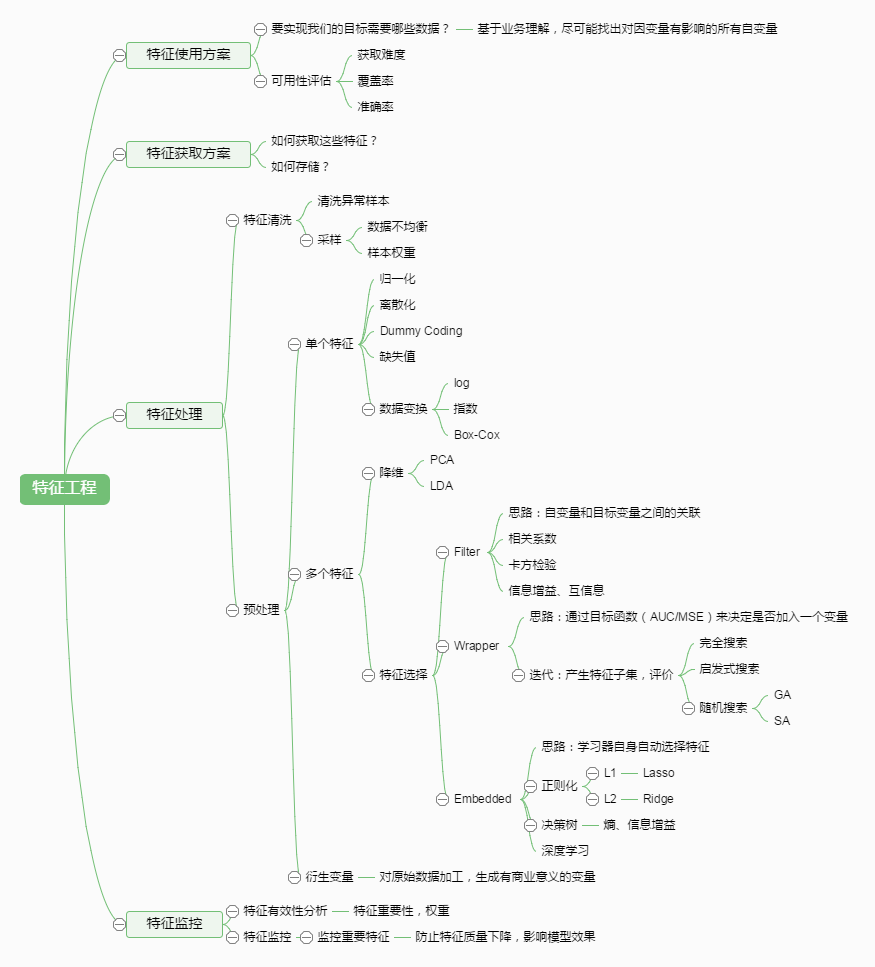
提取就是通过降维技术来抽出主要信息//是计算机视觉的概念,通过映射实现,可以理解为高维的映射到低维,不删除具体特征,而是舍去那些通过映射后不能代表原来主要信息的数据 选择就要舍去一些特征,拿到整体主要特征//要删除一些特征
二者是直接关联的关系.
一般认为, 特征选择是指在拿到一堆原始数据的伪时候,选取有用的feature,以备进行机器学习使用。
比如你拿到的是文本信息,那么里面的单词就是原始数据了, 那么你要考虑的是,数字保留不保留?大小写要不要区分?一些常用词比如of, on, by之类的要不要扔掉?等等。对于图像处理和视频处理也有一套相应的规范和实践。通过下面即将要讲的方法,就可以知道怎么来选择特征和舍去特征。
而特征提取(extract),比如咋做图像识别的时候,由于一个像素表示一个特征的话,现在的照片随随便便就1024*1024像素的,这时候我们就要通过特征提取的方法来抽出最能代表这张照片的主要信息。特征提取(extract)的方法有很多,主要有PCA,PCA的SVD,ICA,还有因子分析(Fachor Analysis)这些讲起来会比较复杂,所以下次要独立一篇再讲一遍(其实也是我现在还没有很好的掌握这些方法-逃。。。)
讲到特征选择,最近有看下天池的一个比赛:Repeat Buyers Prediction,也是现在大三大佬们的大数据作业,任务就是根据用户3个月在天猫的行为日志,建立用户的品牌偏好,并预测他们在将来一个月内对品牌下商品的购买行为。在作业中老师给的特征只是用户之前的行为,所以最终效果真的有点差,百分之五点多的准确率,百分之五点多的召回率,百分之五点多的f1得分,嗯,我纯靠猜都可能比它强吧。。。
所以我去下载了下官网的数据,做了下数据的简单可视化,在用户的年龄段(age range)和性别(gender)方面是很大影响的,具体图如下
然后还有就是商品的类别和品牌也应该是有有影响的(这个想想就能理解了吧),但由于给我的数据量太大了,本来想做可视化折线图的,运行他就,效果也不明显也就放弃了。
具体经过特征添加后的最终结果,我想应该会在回归那篇讲讲(之后写)
在我的项目中,有用到卡方检验来提取特征词,然后来减少无关特征,达到特征选择的目的,实践证明,确实好用!
嗯,有点抽象,那就来结合例子来理解:–以下例子来自《数学之美》(是本好书)。
假设我错过了某年的世界杯比赛,现在要去问一个知道比赛结果的朋友“哪支球队最终获得世界杯冠军”?他要求我猜,猜完会告诉我是对还是错,但我每猜一次就要给他一块钱。那么我需要付给他多少钱才能知道谁是冠军?我可以把球队编号,从1到32,然后问“冠军的球队在1-16号中吗?”。假如他告诉我对了,我就问“冠军的球队在1-8号中吗?”。如果他告诉我不对,我就自然就知道冠军队在9-16号中。这样我只需要猜5次就可以知道哪支球队是冠军了。所以,“谁是世界杯冠军”这个问题的答案的信息量只值5块钱。
香农用“比特”(bit)来作为信息量的单位。像上边“谁是世界杯冠军”这个问题的答案的信息量是5比特。如果是64支球队,“谁是世界杯冠军”这个问题的答案的信息量就是6比特,因为我还要多猜一次。
对足球了解的朋友看到这有疑问了,他觉得他不需要5次来猜。因为他知道巴西,西班牙,德国等这些强队夺冠的可能性比日本,韩国等球队大的多。所以他可以先把强队分成一组,剩下的其它队伍一组。然后问冠军是否在夺冠热门组里边。重复这样的过程,根据夺冠的概率对剩下的候选球队分组,直至找到冠军队。这样也许三次或四此就猜出结果了。因此,当每支球队夺冠的可能性(概率)不一样时,“谁是世界杯冠军”这个问题的答案的信息量比5比特少。
香农指出,“谁是世界杯冠军”这个问题的答案的信息量是:
H = -(p1*log(p1) + p2 * log(p2) + ... + p32 * log(32)), 其中log是以2为底数的对数,以下本文中的log都是以2为底的对数,下边不再特别说明。这就是衡量信息量多少的公式,它的单位是比特。之所以称为熵是因为它的定义形式和热力学的熵有很大的相似性。对于一个随机变量X的信息熵的定义公式为:
H(X)=-∑P(xi)logP(xi),其中xi是随机变量X的可能取值。
应该比较好懂了吧,我就是这样看懂的
信息熵计算:
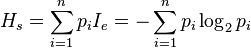
信息熵图:
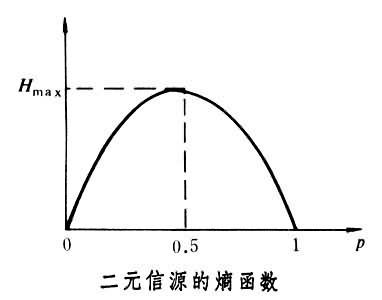
可以看到,在p=0.5(意味着在二元中概率事件发生概率相等的情况下)的时候熵值是最大的,也就是说这个时候是是确定性最低的,最混乱的。(延伸到在足球的例子中的意思就是每个队的获胜概率都相等的时候,那个时候信息量(熵)最大,你就越难猜那个队会赢)
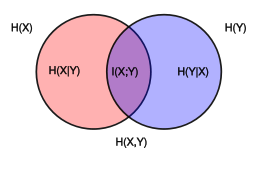
H(Y|X) 表示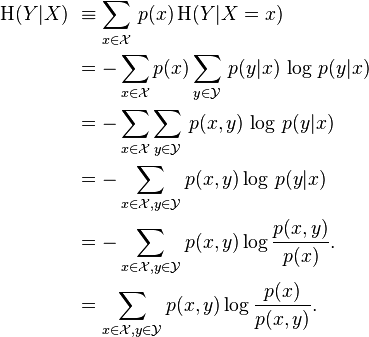
咦,看到上面式子就想起条件概率,其实,条件熵可以类比条件概率,他表示:在随机变量 X 的基础上我们引入随机变量 Y,假设 Y 和 X 有一定的关系。那么 Y 的信息熵会相对减小。
条件熵还是很好理解的吧!不理解吗?还是结合足球的例子,比如你知道其中一个队是铁定不会赢的了,那你要现在要猜那个队会赢,那个难度就下降了是吧,因为信息熵下降了!
知道条件熵之后,信息增益就很简单了,他就是:g(X,Y) = H(X) – H(X|Y),表示的就是条件熵和原来熵的差值
嗯,概念就讲到这里,之后我会写决策树的博文,到时还会复习一下信息熵。介绍一下信息增益比的概念
关于信息论对ML的一些概念,可以看下这篇博文

应该不难理解,但这里有一个问题:
问:《数学之美》 上面 互信息 的公式是:I(X;Y)=H(X)-H(X|Y);又看到 《统计学习方法》 上有一个 信息增益 的公式:G(D,A)=H(D)-H(D|A)。这不是一样吗?难道互信息就是信息增益?
答:IG(信息增益)有两种定义。。一般IG是指KL散度(相对熵)
但在Desicion Tree(决策树)的IG一般是指KL散度的期望,然后正好就是互信息了,其实我想就简单理解并记住计算互信息的公式,然后在机器学习中信息增益是一种特殊的情况,就是她是KL散度的期望。
先看p对q的相对熵为
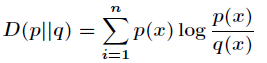
然后是KL散度的期望=互信息
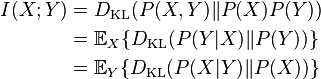
总结:其实信息论要讲起来是一门挺深的课。而我是想用最简单的方式理解最多的知识,可能讲的比较粗略,有兴趣的小伙伴可以看看信息论的书! 最后,用一张图结束:
one-hot编码:大多使用一些线性的算法,它的稀疏格式是记忆友好的(便于存储),注意去掉第一列避免共线性
哈希编码:它是对固定长度的数组进行 Onehot 编码,它避免极度稀疏的数据,但可能会产生冲突
标签编码:它给每个类一个独一无二的数字化 ID,它对于对于非线性的基于树模型的算法很有用,它不增加维度
Count 编码:Replace categorical variables with their count in the train set,它对线性或非线性的算法都适用,对对异常值敏感,Replace unseen variables with 1
LabelCount 编码:Rank categorical variables by count in train set,对线性或非线性算法都适用,它对异常值不敏感
在这里讲述的是常见的几种编码方式,其实还有其他的各种不同的编码,具体请看
Can be more readily fed into algorithms,Can constitute floats, counts, numbers and Easier to impute missing data.
把数字化变量放入箱中,并用 bin-ID 编码,用分位数装箱是很实用的,甚至可以用模型找出可选的箱 可以优雅的找到训练集范围外的变量
特征离散化有两种划分方式:一种是等值划分(按照值域均分),另一种是等量划分 (按照样本数均分)。我们对 numeric 类型的特征采用了等量划分的离散化方式:先将每 一维特征按照数值大小排序,然后均匀地划分为 10 个区间,即离散化为 1~10。
坊间戏言“特征没做好,参数调到老”,机器学习大牛 Andrew Ng 也说过“‘Applied machine learning’is basically feature engineering”,可见特征工程的重要性,我们要在在这部分投入了大量的时间和精力。下面先讲讲怎么来对特征进行处理
one-hot编码:大多使用一些线性的算法,它的稀疏格式是记忆友好的(便于存储),注意去掉第一列避免共线性
哈希编码:它是对固定长度的数组进行 Onehot 编码,它避免极度稀疏的数据,但可能会产生冲突
标签编码:它给每个类一个独一无二的数字化 ID,它对于对于非线性的基于树模型的算法很有用,它不增加维度
Count 编码:Replace categorical variables with their count in the train set,它对线性或非线性的算法都适用,对对异常值敏感,Replace unseen variables with 1
LabelCount 编码:Rank categorical variables by count in train set,对线性或非线性算法都适用,它对异常值不敏感
在这里讲述的是常见的几种编码方式,其实还有其他的各种不同的编码,具体请看
Can be more readily fed into algorithms,Can constitute floats, counts, numbers and Easier to impute missing data.
把数字化变量放入箱中,并用 bin-ID 编码,用分位数装箱是很实用的,甚至可以用模型找出可选的箱 可以优雅的找到训练集范围外的变量
特征离散化有两种划分方式:一种是等值划分(按照值域均分),另一种是等量划分 (按照样本数均分)。我们对 numeric 类型的特征采用了等量划分的离散化方式:先将每 一维特征按照数值大小排序,然后均匀地划分为 10 个区间,即离散化为 1~10。
排序特征对异常数据都有较强的鲁棒性,使得模型更加稳定,降低过拟合的风险。
前面已经对特征进行了离散化,以 uid 为 1 的样本为这次就讲到这里吧,之后我会继续写好下面的博文,希望在写博文的同时,可以加深理解,一起加油!!!例,离散化后它的特征是 5,3,1,3,3,3,2,4,3,2,5,3,2,3,2…2,2,2,2,2,2,2,可以进一步统计离散特征中 1~10 出现的次数 n i (i=1,2,…,10),即可得到一个 10 维计数特征。基于这 10 维特征训练了 xgboost 分类器,线 上得分是 0.58 左右,说明这 10 维特征具有不错的判别性。
赛题数据含有 93 维类别特征,很多算法(如逻辑回归,SVM)只能处理数值型特征, 这种情况下需要对类别特征进行编码,我们采用了 One-Hot 编码,得到了 01 特征,解决 了分类器不能处理类别特征的问题。
| 当不清楚这个编码的时候,你就很有可能会犯错误,例如颜色属性可能会用{1,2,3}表示{红,绿,蓝}。这里存在两个问题:首先,对于一个数学模型,这意味着某种意义上红色和绿色比和蓝色更“相似”(因为 | 1-3 | > | 1-2 | )。除非你的类别拥有排序的属性(比如铁路线上的站),这样可能会误导你的模型。 |
交叉特征算是特征工程中非常重要的方法之一了,交叉特征是一种很独特的方式,它将两个或更多的类别属性组合成一个。当组合的特征要比单个特征更好时,这是一项非常有用的技术。数学上来说,是对类别特征的所有可能值进行交叉相乘。
假如拥有一个特征A,A有两个可能值{A1,A2}。拥有一个特征B,存在{B1,B2}等可能值。然后,A&B之间的交叉特征如下:{(A1,B1),(A1,B2),(A2,B1),(A2,B2)},并且你可以给这些组合特征取任何名字。但是需要明白每个组合特征其实代表着A和B各自信息协同作用。
一个更好地诠释好的交叉特征的实例是类似于(经度,纬度)。一个相同的经度对应了地图上很多的地方,纬度也是一样。但是一旦你将经度和纬度组合到一起,它们就代表了地理上特定的一块区域,区域中每一部分是拥有着类似的特性。
排序特征对异常数据都有较强的鲁棒性,使得模型更加稳定,降低过拟合的风险。
前面已经对特征进行了离散化,以 uid 为 1 的样本为例,离散化后它的特征是 5,3,1,3,3,3,2,4,3,2,5,3,2,3,2…2,2,2,2,2,2,2,可以进一步统计离散特征中 1~10 出现的次数 n i (i=1,2,…,10),即可得到一个 10 维计数特征。基于这 10 维特征训练了 xgboost 分类器,线 上得分是 0.58 左右,说明这 10 维特征具有不错的判别性。
赛题数据含有 93 维类别特征,很多算法(如逻辑回归,SVM)只能处理数值型特征, 这种情况下需要对类别特征进行编码,我们采用了 One-Hot 编码,得到了 01 特征,解决 了分类器不能处理类别特征的问题。
| 当不清楚这个编码的时候,你就很有可能会犯错误,例如颜色属性可能会用{1,2,3}表示{红,绿,蓝}。这里存在两个问题:首先,对于一个数学模型,这意味着某种意义上红色和绿色比和蓝色更“相似”(因为 | 1-3 | > | 1-2 | )。除非你的类别拥有排序的属性(比如铁路线上的站),这样可能会误导你的模型。 |
交叉特征算是特征工程中非常重要的方法之一了,交叉特征是一种很独特的方式,它将两个或更多的类别属性组合成一个。当组合的特征要比单个特征更好时,这是一项非常有用的技术。数学上来说,是对类别特征的所有可能值进行交叉相乘。
假如拥有一个特征A,A有两个可能值{A1,A2}。拥有一个特征B,存在{B1,B2}等可能值。然后,A&B之间的交叉特征如下:{(A1,B1),(A1,B2),(A2,B1),(A2,B2)},并且你可以给这些组合特征取任何名字。但是需要明白每个组合特征其实代表着A和B各自信息协同作用。
一个更好地诠释好的交叉特征的实例是类似于(经度,纬度)。一个相同的经度对应了地图上很多的地方,纬度也是一样。但是一旦你将经度和纬度组合到一起,它们就代表了地理上特定的一块区域,区域中每一部分是拥有着类似的特性。
。损失函数是 f (X)和Y的非负实值函数,记作L(Y, f (X)) . 在李航博士《统计学习方法》中有很详细的介绍,我就偷偷懒,就直接贴下那篇图片好啦,然后简单说明下(哈哈,逃。。)

损失函数的期望是
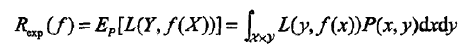
期望风险Rexp(f)是模型关于联合分布的期望损失,经验风险Remp(f)是模型关于训练样本集的平均损失(也就是概率中是实验数据越大,越能代表一般规律)。根据大数定律,当样本容量N趋于无穷时,经验风险趋于期望风险。所以一个很自然的想法是用经验风险估计期望风险。但是,由于现实中训练样本数目有限,甚至很小,所以用经验风险估计期望风险常常并不理想,要对经验风险进行一定的矫正.

当样本容量足够大时,经验风险最小化能保证有很好的学习效果。例:极大似然估计(maximum likelihood estimation)。但是,当样本容量很小时,经验风险最小化学习的效果就未必很好,会产“过拟合(over-fitting)”现象.这就引出下面的正则化。
参考资料:
《统计学习方法》-李航
《机器学习》-周志华
《机器学习实战》-Peter Harrington
斯坦福大学公开课-机器学习
网上的各位大牛的博文