欢迎在文章下方评论，建议用电脑看
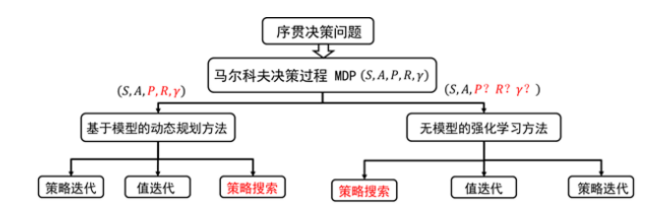
在值函数的方法中，我们迭代计算的是值函数，然后根据值函数对策略进行改进；而在策略搜索方法中，我们直接对策略进行迭代计算，也就是迭代更新参数值，直到累积回报的期望最大，此时的参数所对应的策略为最优策略。
在正式讲解策略搜索方法之前，我们先比较一下值函数方法和直接策略搜索方法的优缺点。其实正因为直接策略搜索方法比值函数方法拥有更多的优点，我们才有理由或才有动机去研究和学习及改进直接策略搜索方法：
（1） 直接策略搜索方法是对策略进行参数化表示，与值函数方中对值函数进行参数化表示相比，策略参数化更简单，有更好的收敛性。
（2） 利用值函数方法求解最优策略时，策略改进需要求解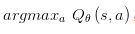
，当要解决的问题动作空间很大或者动作为连续集时，该式无法有效求解。
（3） 直接策略搜索方法经常采用的随机策略，能够学习随机策略。可以将探索直接集成到策略之中。
当然与值函数方法相比，策略搜索方法也普遍存在一些缺点，比如：
（1） 策略搜索的方法容易收敛到局部最小值。
（2） 评估单个策略时并不充分，方差较大。
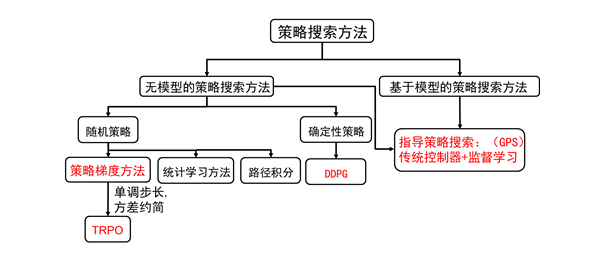
策略搜索方法按照是否利用模型可以分为无模型的策略搜索方法和基于模型的策略搜索方法。
其中无模型的策略搜索方法根据策略是采用随机策略还是确定性策略分为随机策略搜索方法和确定性策略搜索方法。
随机策略搜索方法最先发展起来的是策略梯度方法；然而策略梯度方法存在着学习速率难以确定等问题，为了解决这个问题学者们提出了基于统计学习的方法，基于路径积分的方法，回避学习速率问题。
而TRPO并没有回避这个问题，而是找到了替代损失函数，利用优化方法局部找到使得损失函数单调的步长
简单到不行，而且某些简单场景效果拔群，参见文章（Tetris是俄罗斯方块） Learning Tetris with the Noisy Cross-Entropy Method
算法也很简单
意思就是，根据episodic的rewards排序，选top p%的policy parameters称之为elite set, 做gaussian distribution fitting，得到elite set的policy parameter的mean和variance。据此mean 和 variance产生新的一组policy parameter, 再做评估，选出top p%，以此类推。 采用evolution的思想，淘汰表现不好的策略，让表现好的策略繁衍出更好的策略，再做淘汰，以此类推，这就是CEM。
