

欢迎在文章下方评论,建议用电脑看
提出一个全新的G的目标函数。并用于NLP中,结合了比之前的MC更好的一种减小方差的方法,使得效果更好。
在这篇论文的背景和其他GAN FOR NLP一样都是讲述了一些进程。不过有点不同的是这篇论文和之前的Boundary-Seeking Generative Adversarial Networks是一起的,也就是这里的G的目标函数和那里的是一样的。
下面简单的讲述那个构造函数的由来。
这个BGAN的Intuition就是:令G去学习如何生成在D决策边界的样本,所以才叫做boundary-seeking。作者有一个特别的技巧:如图,当D达到最优的时候,满足如下条件,Pdata是真实的分布,Pg是G生成的分布。
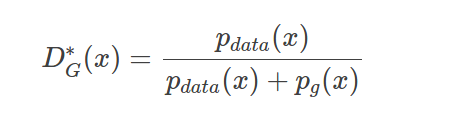
我们对它进行一点微小的变换:这个形式厉害之处在于,尽管我们没有完美的G,但是仍然可以通过对Pg赋予权重来得到真实的分布,这个比例就是如图所示,基于该G的最优D和(1-D)之比。当然我们很难得到最优的D,但我们训练的D越接近最优D,bias越低。而训练D(标准二分类器)要比G简单得多,因为G的目标函数是一个会随着D变动而变动的目标。
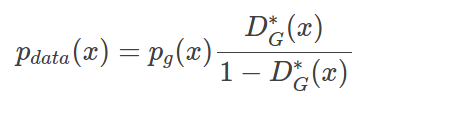
在BGAN这篇文章中给出了一些解释

而在maliGAN中,应用了这种G函数。

其实在一开始的BGAN中,作者就有讲它应用在Discrete variables中,只是在这个的话,没有长序列的生成,但在maliGAN中,扩展到生成序列中,需要解决的问题就是减小方差的呃问题。
这个网路的结构和之前GAN差别不大,也就是在这篇论文中,主要的还是在算法上的改进吧。

这篇论文的主要贡献如下:
1.为G构造一个全新的目标函数,用到了Importance Sampling,将其与D的output结合起来,令训练过程更加稳定同时梯度的方差更低。尽管这个目标函数和RL的方法类似,但是相比之下更能够降低estimator的方差(强烈建议看原文的3.2 Analysis,分析了当D最优以及D经过训练但并没有到最优两种情况下,这个新的目标函数仍然能发挥作用)
2.生成较长序列的时候需要用到多次random sampling,所以文章还提出了两个降低方差的技巧:第一个是蒙特卡罗树搜索,这个大家都比较熟悉; 第二个受到这个文章的启发Sequence level training with recurrent neural networks文章称之为Mixed MLE-Mali Training,就是从真实数据中进行抽样,若序列长度大于N,则固定住前N个词,然后基于前N个词去freely run G产生M个样本,一直run到序列结束。
基于前N个词生成后面的词的原因在于条件分布Pd比完整分布要简单,同时能够从真实的样本中得到较强的训练信号。然后逐渐减少N(在实验三中N=30, K=5, K为步长值,训练的时候每次迭代N-K)
作者给出了实验数据,比SeqGAN的效果要更好,看BLEU score.
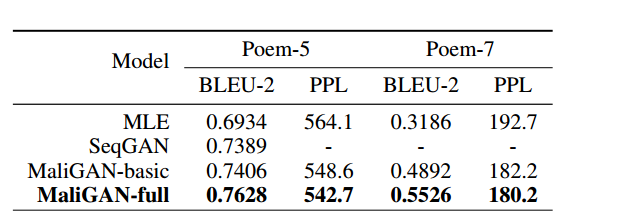
主要是在RL和这个不同方法上进行讨论,之前的RL方法存在的梯度难以从D传到G和本身的不稳定。现在作者提出了一种新的方式来做。这个文章在作者看来就是在用RL类似的方法,用importance sampling+mixed training