欢迎在文章下方评论，建议用电脑看
Karpathy的blog中提到说更多的人更倾向于Policy Gradient.原因如下：
基于值函数的方法（Q-learning, SARSA等等经典强化学习研究的大部分算法）存在策略退化问题，即值函数估计已经很准确了，但通过值函数得到的策略仍然不是最优。这一现象类似于监督学习中通过后验概率来分类，后验概率估计的精度很高，但得到的分类仍然可能是错的。尤其是当强化学习使用值函数近似时，策略退化现象非常常见。可见 Tutorial on Reinforcement Learning slides中的例子。Policy Gradient不会出现策略退化现象，其目标表达更直接，求解方法更现代，还能够直接求解stochastic policy等等优点更加实用。
我们已经知道DQN是一个基于价值value的方法。换句话说就是通过计算每一个状态动作的价值，然后选择价值最大的动作执行。这是一种间接的做法。那么，更直接的做法是什么？
能不能直接更新策略网络Policy Network呢？
什么是策略网络Policy Network？就是一个神经网络，输入是状态，输出直接就是估计动作（不是Q值）。这里的label就是真实动作,loss就是:所选概率的-log值*（本reward + 衰减的未来reward）
要更新策略网络，或者说要使用梯度下降的方法来更新网络，我们需要有一个目标函数。对于策略网络，目标函数其实是比较容易给定的，就是很直接的，最后的结果！也就是
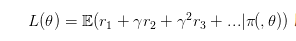所有带衰减reward的累加期望
那么问题就在于如何利用这个目标来更新参数\theta呢？咋一看这个损失函数和策略网络简直没有什么直接联系，reward是环境给出的，如何才能更新参数？换个说法就是如何能够计算出损失函数关于参数的梯度（也就是策略梯度）：
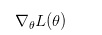
Policy gradient 是 RL 中另外一个大家族, 他不像 Value-based 方法 (Q learning, Sarsa), 但他也要接受环境信息 (observation), 不同的是他要输出不是 action 的 value, 而是具体的那一个 action, 这样 policy gradient 就跳过了 value 这个阶段. 而且个人认为 Policy gradient 最大的一个优势是:输出的这个 action 可以是一个连续的值, 之前我们说到的 value-based 方法输出的都是不连续的值, 然后再选择值最大的 action,如果动作很多的话，这样贪婪策略来选择变得很不现实. 而 policy gradient 可以在一个连续分布上选取 action.这样对于动作众多或者连续动作的是很可行的
改变动作的出现概率！ 现在我们不考虑别的，就仅仅从概率的角度来思考问题。我们有一个策略网络，输入状态，输出动作的概率。然后执行完动作之后，我们可以得到reward，或者result。那么这个时候，我们有个非常简单的想法：
如果某一个动作得到reward多，那么我们就使其出现的概率增大，如果某一个动作得到的reward少，那么我们就使其出现的概率减小。 当然，也显然的，用reward来评判动作的好坏是不准确的，甚至用result来评判也是不准确的。毕竟任何一个reward，result都依赖于大量的动作才导致的。但是这并不妨碍我们做这样的思考：
如果能够构造一个好的动作评判指标，来判断一个动作的好与坏，那么我们就可以通过改变动作的出现概率来优化策略！
假设这个评价指标是f(s,a),那么我们的Policy Network输出的是概率。一般情况下，更常使用log likelihood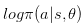 
。原因的话看这里Why we consider log likelihood instead of Likelihood in Gaussian Distribution。
简单说明：其实要用log的主要原因就是我们之后要用到极大似然的方式来求，一个是比较好算，第二是这样才不会造成计算的溢出。
因此，我们就可以构造一个损失函数如下：
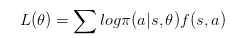
怎么理解呢？举个简单的AlphaGo的例子吧。对于AlphaGo而言，f(s,a)就是最后的结果。也就是一盘棋中，如果这盘棋赢了，那么这盘棋下的每一步都是认为是好的，如果输了，那么都认为是不好的。好的f(s,a)就是1，不好的就-1。所以在这里，如果a被认为是好的，那么目标就是最大化这个好的动作的概率，反之亦然。
这就是Policy Gradient最基本的思想。
f(s,a)不仅仅可以作为动作的评价指标，还可以作为目标函数。就如同AlphaGo，评价指标就是赢或者输，而目标就是结果赢。这和之前分析的目标完全没有冲突。因此，我们可以利用评价指标f(s,a)来优化Policy，同时也是在优化的同时优化了f(s,a).那么问题就变成对f(s,a)求关于参数的梯度。下面的公式直接摘自Andrej Karpathy的blog，f(x)即是f(s,a)
从公式得到的结论可以看到正好和上一小结分析得到的目标函数一致。
最后，来自莫烦python的一张图,那里的例子比较好懂，值得一看。下面也是基本的Policy Gradient的算法。
其实，这个也就是那个课程上的Monte-Carlo Policy Gradient
