欢迎在文章下方评论，建议用电脑看
简单来说，function approximation的意义是： large MDPs 的情况下，如果算出每种状态下的真实value function既没有足够的内存也没有足够的计算能力，此外比较接近的状态它们的值函数取值应该是很相似的，这是一种泛化能力。也就是说需要算法来求解近似的V(S)和Q(S,A)，并且针对未知的状态有比较强的泛化能力。这种近似算法称之为function approximation.
假设近似值函数对w是可微的，最简单的就是用梯度下降，假设输入状态用特征向量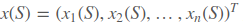
，例如机器人的行走状态，第一个特征是距离横向基准位置多远，第二个特征是距离纵向基准位置多远等等。损失函数是
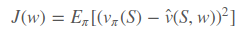。从而随机梯度下降求得权重改变量为
。
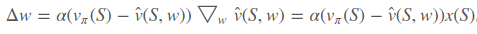但是在强化学习中，vπ(S)是未知的，无法用来当做监督信息，因此要用别的东西来代替，从而可以根据Monte-Carlo Learning和Temporal Difference Learning两种方法来考虑。
Monte-Carlo Learning中针对某个状态叠加每个episode中在这个状态上产生的return，因为每个episode是走到了终止状态的，所以可以向初始状态的方向将return传播回来。而实际上值函数就是return的期望，所以基于MC方法就是用GtGt代替vπ(S)
Temporal Difference Learning中针对某个状态估计下一个时刻可能获得的return，由immdiate reward和上一次更新的值函数构成，也称为TD target，从而更新当前时刻的值函数，因此用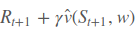
来替换vπ(S)vπ(S)。替换后发现括号内的这一项就是TD error。同样的TD(λ)也是替换成第四课的公式即可。
也就是替换成下面的误差函数
而动作值函数也是差不多的，就是替换，这里就不提了，参考[1]。
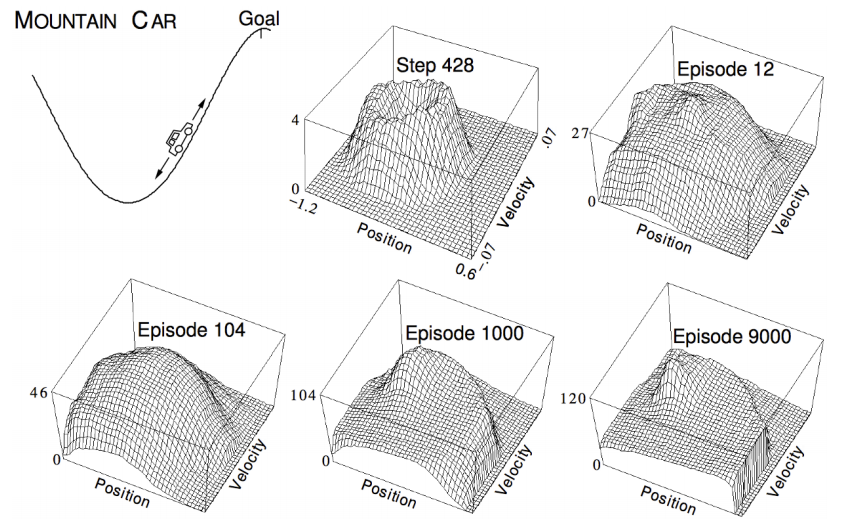
在强化学习中，有个比较经典的例子就是汽车爬山[2]，车会在凹的山谷中来回启动，不同的高度上汽车需要学会利用势能来到达对面的山顶，这个问题中的状态就是汽车所处的位置和当前的速度(个人觉得当前的速度应该是action，在不同的位置人控制不同的速度，但是David课中说action是选择加速还是不加速)，曲面的起伏代表了value function。通过图中多执行多个episode得到了值函数的表达形式。
此处讲batch methods说”梯度下降的方法针对一个sample，只利用一次，更新一次梯度之后就不再使用了，并没有挖掘出这个sample所有信息，因此需要用batch methods来重复的利用sample并找到最佳拟合值函数，拟合所有看到过的sample” ，这个意思我觉得并不重要，如果用神经网络来学习参数必然会多次迭代sample，所以直接介绍DQN。
最后十分钟讲了一下如何结合最小二乘法与MC/TD，令导数等于0再推导，流程跟梯度下降一样，这里就不提了，经过这几课大致可以看出强化学习要求解的核心就是policy和值函数，这一课可以看出值函数的具体形式可以用神经网络表示出来，即把状态变换成一个特征向量当做输入，经过神经网络得到值函数输出。
