

欢迎在文章下方评论,建议用电脑看
输入:样本S = X1, X2,…, Xm。 步骤:
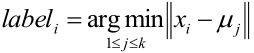
PS:上式的读法是:样本xi的类别距离xi最近的聚类中心μj的那个类别。 3. 经过上面一步,有些聚类(聚类集合也称为簇)中的元素就更新了,于是就需要调整聚类中心,所以将每个类别中心更新为隶属该类别的所有样本的均值: <img src="https://yzhihao.github.io/static/img/blog/Machine Learning/base_cluster2.jpg" alt="header1" style="height:auto!important;width:auto%;max-width:1020px;"/>
好了,算法步骤写完了,那我们下面继续讨论几个问题。
* k -means算法一定收敛吗?在特定的场景下,答案是肯定的。 * 可以证明k-means正是在J上的坐标下降过程(参考第八讲)。尤其是k-means算法的内循环实际上是在重复:保持μ不变最小化J关于c的函数,然后再保持c不变最小化J关于μ的函数。因此,J是单调递减的,它的函数值一定收敛
也就是说初始值对结果的影响较大 在聚类的时候要多选几次随机初始化,然后选择最小
步骤知道了,那选择几个类别呢? 这个还真没有好办法,只能使用先验知识选定、拍脑门选一个或者用交叉验证的方式去验证…. 当然有些地方说K=(n/2)1/2,这个知道就好。
话说K-means是初值敏感的,K-means算法会产生局部最优值的。即:如果聚类中心选择的不太好的话,可能到一个不太好的地方后就停了。那如何选择聚类中心呢?有这么个方法:
记K个簇中心为μ1,μ2,…,μk,每个簇的样本数目为N1,N2, …, Nk
使用平方误差作为目标函数:
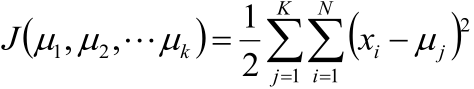
注:上式中等号右边的意思是:求属于第j个簇的所有样本到第j个簇的聚类中心μj的距离的平方和,然后求所有簇的上述值的和。
我们的目的是对该目标函数取最小,哪一个聚类中心,或者说哪一个簇能使该目标函数取最小,我们就说哪个是最好的。 于是对μ求偏导:

这是在说:
优点:
比如数组1、2、3、4、100的均值为22,显然距离“大多数”数据1、2、3、4比较远。 于是改成求数组的中位数3,在该实例中更为稳妥。 这就是K-Mediods聚类(K中值聚类),它的目标函数一定意义上可以认为是把K-means的目标函数中的平方换成绝对值。 这个算法在一定程度上可以对抗异常值。
从几何上讲,单高斯分布模型在二维空间应该近似于椭圆,在三维空间上近似于椭球。遗憾的是在很多分类问题中,属于同一类别的样本点并不满足“椭圆”分布的特性。这就引入了高斯混合模型。而且因为高斯函数具有良好的计算性能,所以GMM被广泛地应用。
GMM简单的说就是从几个GSM(高斯分布)中生成出来的。即,如果GSM(高斯分布)的概率密度函数用
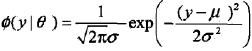 ,θ = (μ,σ2)
表示的话,那GMM就是:
,θ = (μ,σ2)
表示的话,那GMM就是:

其中,ak是系数,ak >=0,
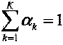
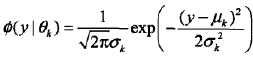
称为第k个分模型,其中θk= (μk,σk2)。a1+a2+…+aK = 1。
假设观测数据y1, y2,…, yN由GMM生成

其中,θ = (a1,a2, …, ak; θ1, θ2, …, θk)。 我们的目标是用EM算法估计GMM的参数θ。
1,明确隐变量,写出完全数据的对数似然函数
| 可以设想观测数据yj,j = 1, 2,…, N,是这样产生的:首先依概率ak选择第k个高斯分布分模型φ(y | θk);然后依第k个分模型的概率分布φ(y | θk)生成观测数据yj。 |
这时观测数据yj是已知的,观测数据yj来自的第k个分模型是未知的(k =1, 2, .., K),于是这个就是隐变量,我们用rjk表示,其定义如下:

PS:隐变量rjk是0-1随机变量。 有了观测数据yj及未观测数据rjk,那么完全数据是 (yj,rj1, rj2, …, rjk), j = 1, 2, …, N 于是,可以写出完全数据的似然函数
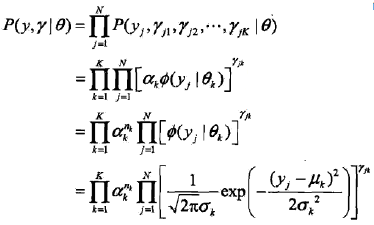
式中
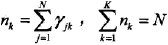 (a式)
(a式)
tip: 第一个等号:在满足θ的高斯分布中,第j样本点出现的概率是P(yj, rj1, rj2, …, rjK | θ),于是代表“所有的样本点出现的概率”的P(y,r | θ)就推出了第一个等号。 第二个等号:由9.27式可得,若第j个观测来自第k个分模型时,rjk=1,即,akφ(yj|θk)]^rjk = akφ(yj|θk)],反之,akφ(yj|θk)]^rjk = 0。 于是将K个akφ(yj|θk)]^rjk连乘,就表示了第j个样本集合属于第k个分模型,即P(yj, rj1, rj2, …, rjK | θ)的展开 后面两个等号是基本的数学知识,就不再解释了。
那么,完全数据的对数似然函数就是
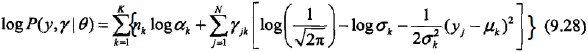
2,EM算法的E步:确定Q函数
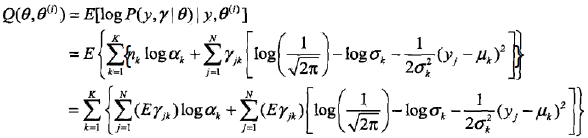
tip: 上面的第三个等号的推导,就是把(a式)中的nk带进去,然后把E放到里面。
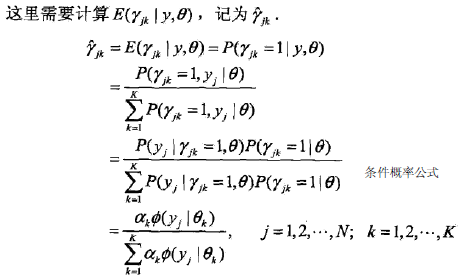
 是在当前模型参数下第j个观测数据来自第k个分模型的概率,称为分模型k对观测数据yi的响应度。
是在当前模型参数下第j个观测数据来自第k个分模型的概率,称为分模型k对观测数据yi的响应度。
最后将
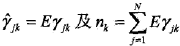
代入9.28式,即得
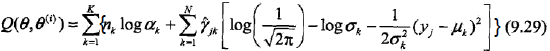
3,确定EM算法的M步
这一步就简单了,Q函数已经知道,即9.29式,那对Q函数中的θ对应的各参数求偏导,并令其为0就可以了,其结果如下:
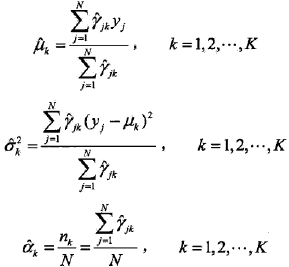
4,重复以上计算,知道对数似然函数不再有明显的变化为止。
方案1:协方差矩阵设为单位矩阵,每个模型比例的先验概率设为相等;均值u设为随机数。
方案 2:由k均值(k-means)聚类算法对样本进行聚类,利用各类的均值作为u,初始的协方差矩阵源自于原始数据的协方差矩阵,且每个簇的初始协方差矩阵相同,取各类样本占样本总数的比例。
我们发现,通常用方案二会取得更好的结果
相同点: (1)需要指定K值 (2)需要指定初始值,例如K-means的中心点,GMM的各个参数 (3)都是含有EM算法思想
不同点: (1)优化目标函数不同,K-means:最短距离,GMM:最大化log似然估计 (2)E步的指标不同,K-means:点到中心的距离(硬指标),GMM:求解每个观测数据的每个component的概率(软指标)
参考资料:
《统计学习方法》-李航
《机器学习》-周志华
《机器学习实战》-Peter Harrington
斯坦福大学公开课-机器学习
网上的各位大牛的博文