24 Feb 2017

关联分析(二)_FP-growth算法

关联分析(二)–FP-growth算法

FP-growth算法将数据存储在一种称为FP树的紧凑数据结构中。FP（Frequent Pattern）通过链接来连接相似元素，被连起来的元素项可以看成一个链表。

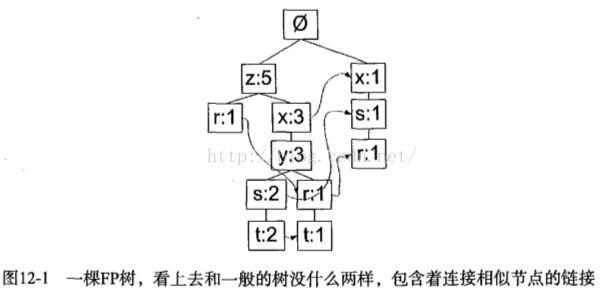
header1

同搜索树不同的是，一个元素项可以在一棵FP树中出现多次。FP树会存储项集的出现频率，而每个项集会以路径的方式存储在树中。存在相似元素的集合会共享树的一部分。只有当集合之间完全不同时，树才会分叉。树节点上给出集合中的单个元素及其在序列中的出现次数，路径会给出该序列的出现次数。相似项之间的链接即节点链接，用于快速发现相似项的位置。 FP-growth算法首先构建FP树，然后利用它来挖掘频繁项集。为构建FP树，需要对原始数据集扫描两遍。第一遍对所有元素项的出现次数进行计数。第二遍扫描只考虑那些频繁元素。

构建FP树

除了FP树的类，还需要头指针表来指向给定类型的第一个实例。通过头指针表可以快速访问FP树中一个给定类型的所有元素。可用字典保存，并且其value存放FP树中每类元素的总数。

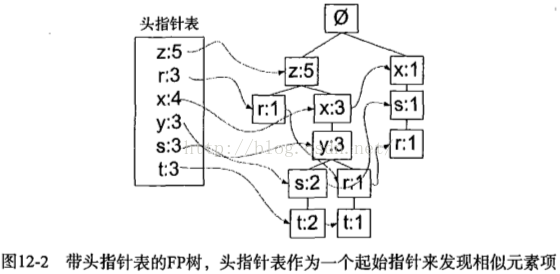
header1

第一遍遍历数据集得到每个元素项的出现频率。去掉不满足最小支持度的元素项。再构建FP树。构建时，读入每个项集并将其添加到一条已经存在的路径中。如果该路径不存在，则创建一条新路径。每个事务就是一个无序集合。假设集合{z,x,y}和{y,z,r}，那么在FP树中，相同项只会表示一次。为此在将集合添加到树之前，先对每个集合进行排序，排序基于元素项出现的频率。

header1

在对事务记录过滤和排序之后，就可以构建FP树了。从空集，向其中不断添加频繁项集。过滤、排序后的事务依次添加到树中，如果树中巳存在现有元素，则增加现有元素的值;如果现有元素不存在，则向树添加一个分枝。

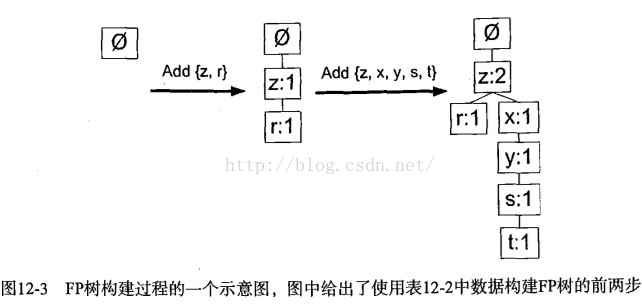
header1

从一颗FP树中挖掘频繁项集

有了FP树之后，就可以抽取频繁项集了，首先从单元素项集开始，然后在此基础上逐步构建更大的集合。

步骤：

从FP树中获得条件模式基;
利用条件模式基，构建一个条件FP树;
迭代重复步骤1,2，直到树包含一个元素项为止。

抽取条件模式基

条件模式基是以所查找元素项为结尾的路径集合。每一条路径其实都是一条前缀路径。图12-2中，符号r的前缀路径有{x,s},{z,x,y}和{z}。根据头指针表通过上溯树直到根节点抽取出条件模式基。

header1

由前缀再创建条件FP树 对于每一个频繁项，都要创建一颗条件FP树。通过递归可发现频繁项、条件模式基以及另外的条件树。假设以频繁项t创建一个条件FP树，然后对{t,y}、{t,x}、…等重复该过程。

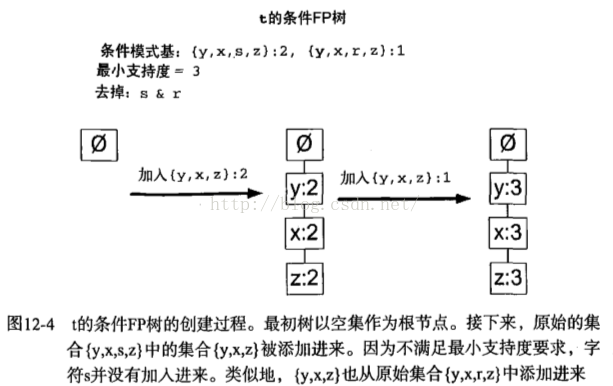
header1

恩，也不是特别的难是吧，下面再补充一个详细例子，主要注意的就是在用频繁项递归构建FP树那里要注意一下就好了！

算法原始数据如下：

1、I5的条件模式基是(I2 I1:1), (I2 I1 I3:1)，I5构造得到的条件FP-树如下。然后递归调用FP-growth，模式后缀为I5。这个条件FP-树是单路径的，在FP_growth中直接列举{I2:2，I1:2，I3:1}的所有组合，之后和模式后缀I5取并集得到支持度>2的所有模式：{ I2 I5:2, I1 I5:2, I2 I1 I5:2}。

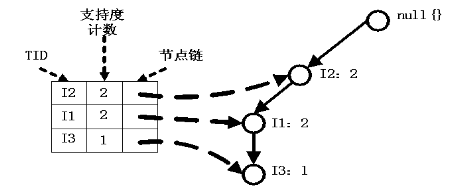
header1

2、I5的情况是比较简单的，因为I5对应的条件FP-树是单路径的，我们再来看一下稍微复杂一点的情况I3。I3的条件模式基是(I2 I1:2), (I2:2), (I1:2)，生成的条件FP-树如左下图，然后递归调用FP-growth，模式前缀为I3。I3的条件FP-树仍然是一个多路径树，首先把模式后缀I3和条件FP-树中的项头表中的每一项取并集，得到一组模式{I2 I3:4, I1 I3:4}，但是这一组模式不是后缀为I3的所有模式。还需要递归调用FP-growth，模式后缀为{I1，I3}，{I1，I3}的条件模式基为{I2：2}，其生成的条件FP-树如右下图所示。这是一个单路径的条件FP-树，在FP_growth中把I2和模式后缀{I1，I3}取并得到模式{I1 I2 I3：2}。理论上还应该计算一下模式后缀为{I2，I3}的模式集，但是{I2，I3}的条件模式基为空，递归调用结束。最终模式后缀I3的支持度>2的所有模式为：{ I2 I3:4, I1 I3:4, I1 I2 I3:2}

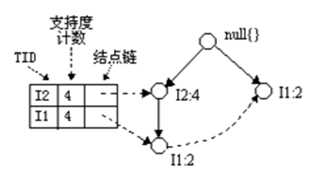
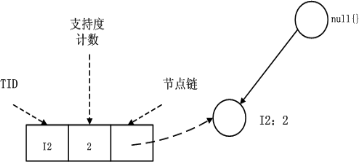
header1