

欢迎在文章下方评论,建议用电脑看
今天我们讲下一个算法,注意,它不是一个模型,而只是一个一般方法,是求解最优值的一个方法!然后,好想吐槽的是,因为em算法比较概率论的问题,但很巧的是,我的概率论下学期才开始学,高中又很多忘记了,所以一开始接触em算法的时候,简直想死。。。感觉它很难理解,非常难以理解,还好,冒着向死而生的思想,我就不行时间的投入,精力的投入,还搞不定它,最后是感谢网上的博文,一点一点的理解,现在应该是有些明白了,但是可能任然有许多比较懵懂,下面我敢但写下这篇博文。。。希望不会被打!
我们常见到的Jensen不等式的版本是: 当φ是凸函数时(φ’’>0):φ( E(x) )<= E(φ(x) ) 不过这里用到的是下面这个版本: 当φ是凸函数时

不太好理解,那我们就拿下面简单的例子来说明: 设有限集合中只有x1和x2,我们很容易发现,当是凸函数的时候(注意:这里的凸函数是外国的概念引入,和我们国内学的凸函数是相反的,下面的我们学的时候是凹函数)φ( E(x) )<= E(φ(x)是一直成立的,当x1=x2的时候,取等号!
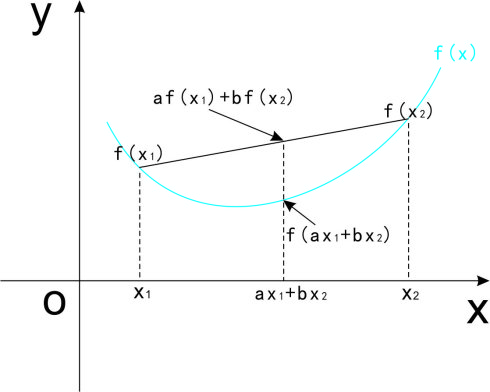
好了,在低维的理解了之后,我们就可以很自然的引申到高维的来理解,其实是一样的!
讲EM算法之前,我们先来看下极大似然估计,这个在与机器学习有关的数学基础——概率论部分这片博文有讲解,而EM算法是为了解决“最大似然估计”中更复杂的情形而存在的。 这里“极大似然估计中更复杂的情形”是什么情形呢? 我们知道极大似然估计是求解实现结果的最佳参数θ,但极大似然估计需要面临的概率分布只有一个或者知道结果是通过哪个概率分布实现的,只不过你不知道这个概率分布的参数。而如果概率分布有多个呢或者你不知道结果是通过哪个概率分布实现的?于是别说去确定“这些概率分布”的最佳参数了,我们连最终结果是根据哪个概率分布得出来的都不知道,这就是EM算法要面临的情况了。
最大似然估计和EM算法都是根据实现结果求解概率分布的最佳参数θ,但最大似然估计中知道每个结果对应哪个概率分布(我知道哪个概率分布实现了这个结果),而EM算法面临的问题是:我不知道哪个概率分布实现了该结果。怎么在不知道其概率分布的情况下还能求解其问题?且看EM算法:
在说明EM算法的求解思想前,我们先总结下上面的内容。
一般的用Y表示观测到的随机变量的数据,Z表示隐随机变量的数据(因为我们观测不到结果是从哪个概率分布中得出的,所以将这个叫做隐变量)。于是Y和Z连在一起被称为完全数据,仅Y一个被称为不完全数据。
这时有没有发现EM算法面临的问题主要就是:有个隐变量数据Z。而如果Z已知的话,那问题就可用极大似然估计求解了。 于是乎,怎么把Z变成已知的?
我先举个日常生活的例子。
结果:大厨把锅里的菜平均分配到两个碟子里
难题:如果只有一个碟子乘菜那就什么都不用说了,但问题是有2个碟子,而因为根本无法估计一个碟子里应该乘多少菜,所以无法一次性把菜完全平均分配。
解法:大厨先把锅里的菜一股脑倒进两个碟子里,然后看看哪个碟子里的菜多,就把这个碟子中的菜往另一个碟子中匀匀,之后重复多次匀匀的过程,直到两个碟子中菜的量大致一样。 上面的例子中,平均分配这个结果是“观测数据”,为实现平均分配而给每个盘子分配多少菜是“待求参数θ”,分配菜的手感就是“概率分布”。于是若只有一个盘子,那概率分布就确定了(“把锅里的菜全部倒到一个盘子”这样的手感是个人都有吧),而因为有两个盘子,所以“给一个盘子到多少菜才好”的手感就有些模糊不定,不过我们可以采用上面的解法来实现最终目标。
理解EM算法最好的方式我觉得就是结合这些类比去理解,然后看下那些数学公式是怎么来的,这样就可以事半功倍了!请看下面:
EM算法的思想就是:
而上面的第二步被称作E步(求期望),第三步被称作M步(求极大化),于是EM算法就在不停的EM、EM、EM….,所以被叫做EM算法,你看,多形象(摊手)。
下面,我们把上面的做法对应到EM算法。从直观上理解,很好明白把!
该来的总会来的,最终我们还是要用数学语言来描述EM算法,那么下面我们看看EM算法的推导过程。
在此先将问题抽象: 已知模型为p(Y|θ),Y=(y1, y2,…, yn),求θ。 为了满足EM算法的情形,我们引入隐含变量Z=(z1, z2, …, zn)。 解: 1,虽然我们面对的概率模型里含有隐变量,但我们的目标是不会变的,即,极大化观测数据(不完全数据)Y关于参数θ的对数似然函数,即,极大化:
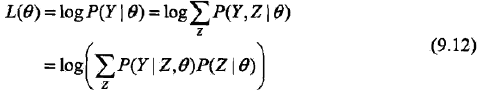
PS:上面式子的第二个等号利用了[边缘概率与联合概率]()方面的知识;第三个等号利用了条件概率公式,于是P(y,z) = P(y|z) P(z),最后把参数θ加上去,即,所有式子都添加θ,就成了9.12式。
2,我们开始对L(θ)进行迭代,使得新的估计值θ能使L(θ)增加,假设现在已经迭代了i次,于是就是使当前的L(θ)大于L(θ(i)),即L(θ) >L(θ(i)),就这样使L(θ)逐步达到最大值。 PS:这就是EM算法中的M步。 为此,我们考虑两者的差:
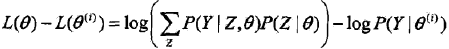
利用Jensen不等式得到其下界:
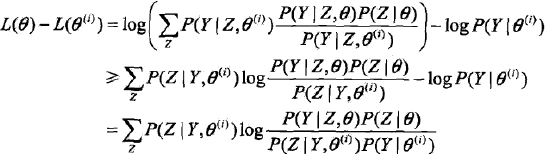
为了便于之后的书写,令
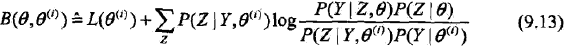
则L(θ)>= B(θ, θ(i)) 即函数B(θ, θ(i))是L(θ)的一个下界。PS:L(θ(i))= B(θ(i), θ(i)) 因此,任何可以使B(θ, θ(i))增大的θ也可以使L(θ)增大。 于是,为了使L(θ)有尽可能大的增长,选择θ(i+1)使B(θ, θ(i))达到极大,即:

现在求θ(i+1)的表达式
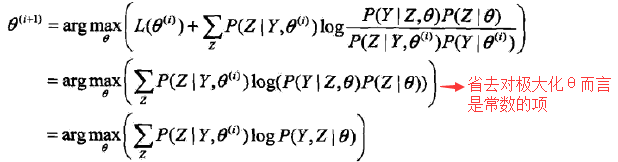
3,为了计算上面的式子,我们就要计算(所以在算法中,这一步在上一步之前)
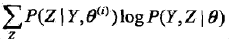
| 而这个就是完全观测数据的对数似然函数logP(Y,Z | θ)关于在给定观测数据Y和当前参数θ(i)下对未观测数据Z的条件概率分布P(Z | Y, θ(i))的期望,这个被称为Q函数,即: |
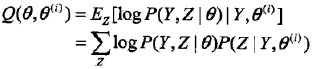
也就是说,要计算期望。 而这,就是EM算法中的E步。
4,不断迭代上面两步,直到收敛。 用图形解释EM算法的推导过程的话就是下面这样:
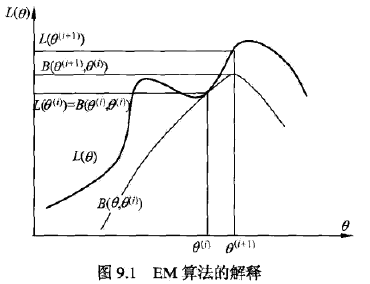
如上图所示,图中上方曲线为L(θ),下方曲线为B(θ, θ(i))。在推导过程中已经知道B(θ,θ(i))是对数似然函数L(θ)的下界,且两个函数在点θ = θ(i)处相等。之后EM算法找到下一个点θ(i+1)使函数B(θ, θ(i))极大化,也使函数Q(θ, θ(i))极大化。这时L(θ) >= B(θ, θ(i)),函数B(θ, θ(i))的增加保证对数似然函数L(θ)在每次迭代中也是增加的。EM算法再点θ(i+1)重新计算Q函数值,进行下次迭代。在这个过程中,对数似然函数L(θ)不断增大。
不过,从图中可以推断出EM算法可能因为陷入局部最优值而找不到全局最优解,并且对初始值是比较敏感的,这点需要注意。
Q函数就是EM算法第二步的Q(θ, θ(i)),我将Q函数单独放在一章是因为Q函数是EM算法的核心。 如果你已经深刻理解了上面的内容,那么会明白,整个EM算法最难的部分就是构建Q函数。为什么?因为EM算法的两步E步和M步在实际应用中就是“构建Q函数”和“通过偏导求极大值”,而后者我想大家都会,于是如何构造前者就是我们需要掌握的技能了。
PS:当然,对于最常用的“高斯混合模型”已经有现成的公式可以套用了。
首先先看下Q函数的定义:
| 完全观测数据的对数似然函数logP(Y,Z | θ)关于在给定观测数据Y和当前参数θ(i)下对未观测数据Z的条件概率分布P(Z | Y, θ(i))的期望称为Q函数,即: |
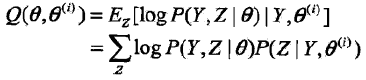
于是你看懂了吗? 反正我一开始没看懂,虽然根据定义知道是求期望,但为了弄懂第二个等号真的用了我一番功夫。
下面我解释下。 首先Q函数是求期望,这个不用多说。 然后,是求什么的期望?为了方面说明,我们把上面的式子的条件给去掉,即Q(θ, θ(i)) = E[logP(Y, Z)]。这下一目了然了,是求函数logP(Y,Z)的期望,而既然是求函数的期望,那就需要用到下面的知识了:

这里使用第一个。 首先对于logP(Y,Z),因为Y是观测变量数据,Z是隐变量数据,因此Z是未知量。所以,对应到上面第一个求法就是:x(变量)=Z,g(x) = g(z) = logP(Y, Z),又因为Q函数的定义中已经告知P(Z| Y, θ(i))是条件概率分布,所以P(Z | Y, θ(i))就对应上面的分布律,不过为了方面说明,这里还是先将条件给去掉,即分布律为P(Z)。 这样一来,套用上面的公式,就有了:
Ez[logP(Y,Z)] = logP(Y,Z)P(Z)
上面为了方面理解而把表示条件的参数都给去掉了,下面按照Q函数的定义把条件给还原回来,于是就有了Q函数定义中的式子。
PS:如果上面还原参数的这步你还有点晕,那就这样想: 联合概率P(Y, Z)是在参数为θ的某分布中,所以为了用公式表述完整,我们将其写成P(Y,Z | θ),分布律P(Z)是在观测变量Y和在EM算法中一步步迭代时当前步骤中已知的“以θ(i)为参数的某分布”下的分布律,所以为了用公式表述完整,我们将其写成P(Z | Y, θ(i))
至于Q函数为什么写成Q(θ, θ(i)),这是因为它想表达:在当前迭代中我要找出一个新θ,使得“以新θ为参数的某分布”优于“用上一次迭代中已找出的θ(i)为参数的某分布”。
坐标上升法(Coordinate ascent):
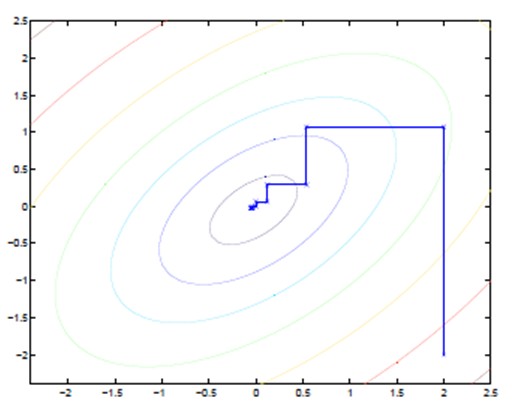
图中的直线式迭代优化的路径,可以看到每一步都会向最优值前进一步,而且前进路线是平行于坐标轴的,因为每一步只优化一个变量。
这犹如在x-y坐标系中找一个曲线的极值,然而曲线函数不能直接求导,因此什么梯度下降方法就不适用了。但固定一个变量后,另外一个可以通过求导得到,因此可以使用坐标上升法,一次固定一个变量,对另外的求极值,最后逐步逼近极值。对应到EM上,E步:固定θ,优化Q;M步:固定Q,优化θ;交替将极值推向最大。
参考资料:
《统计学习方法》-李航
《机器学习》-周志华
《机器学习实战》-Peter Harrington
斯坦福大学公开课-机器学习
网上的各位大牛的博文