

欢迎在文章下方评论,建议用电脑看
p(AB)=P(B)P(A|B)。这个是高中就学过的,不多说!学习机器学习,就不得不学贝叶斯这个东西啦,首先,不要怕,他就是一个条件概率,表面上理解起来很简单!
要学习贝叶斯概率,首先就是要知道全概率公式。全概率公式如下:
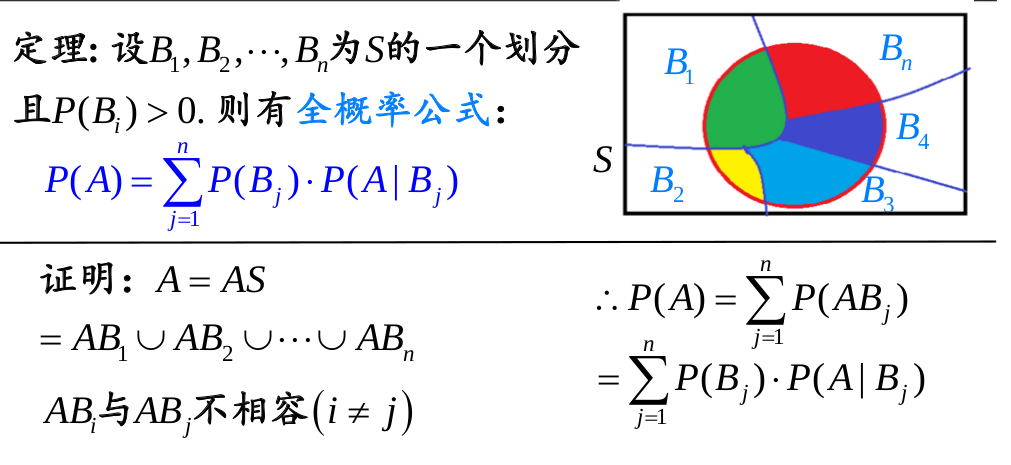
不要着急,如果理解不了下面有例子。

P(A|B) = P(A)P(B|A) / P(B),则P(A):先验概率。即:在的得到新数据前某一假设的概率。 P(A|B):后验概率。即:在看到新数据后,要计算的该假设的概率。 P(B|A):似然度。即:在该假设下,得到这一数据的概率。 P(B):标准化常量。即:在任何假设下得到这一数据的概率。
好了上例子:


随机变量X:为一映射,其自变量具有随机性,就是一个函数,注意:自变量是事件,因变量是事件发生的概率
若随机变量X的取值为有限个或可数,就称X离散,自变量-事件离散。
随机变量X的只可能取0,1 两个值,只有两个可能结果的试验,故称为两点分布有时也称为贝努利分布.
可以理解为只有一次实验,两种可能的值的分布
就是k重伯努利实验的分布中,p发生K次的概率
注意,0-1分布/贝努利分布是二项分布的一种特殊情况,就是n=1的时候
例如:
某人一天内收到的微信的数量
来到某公共汽车站的乘客
某放射性物质发射出的粒子
显微镜下某区域中的白血球
即 当 n >10, p < 0.1 时 , 二项分布 B ( n , p ) 可以用泊松分布pi( np ) 来近似.
在这里,可以这样看:就是当事件多样性多,概率都较低的时候就是泊松分布,否则就是二项分布
就是关于随机变量的函数,也就是关于x<某个值(在离散型表示的就是边界,在连续表示的就是某一个点)的函数
一般地,离散型随机变量的分布函数为阶梯函数,
离散型和连续型分布函数的理解见
两个是相对应的,其性质是相对应的。
两个是一样的,但随机变量表示离散时的事件概率,概率密度表示在某个值的概率。
随机变量就是:事件到概率的映射,密度函数也一样,只不过是极限
随机变量函数就是用随机变量做自变量
连续型结合直线上的例子,注意的是F(x)表示的是概率,面积总和为1,F(x)表示的是概率密度可以大于1,这个值大小满足积分为1,并大于0就可,可以用课件:概率密度和连续型变量的例1
F(x)一定是一个连续函数
直观理解:x落到a,b等长即落入中的的任意子度等区间上是可能的.
概率计算就可以推导出是长度之比
概率密度函数是一个指数阶的
重要的性质,是无记忆性的,这个性质就是唯一的。也就是说看是不是服从指数分布就可以通过是否有无记忆性来指出
打电话的例子:
 答案:
答案:
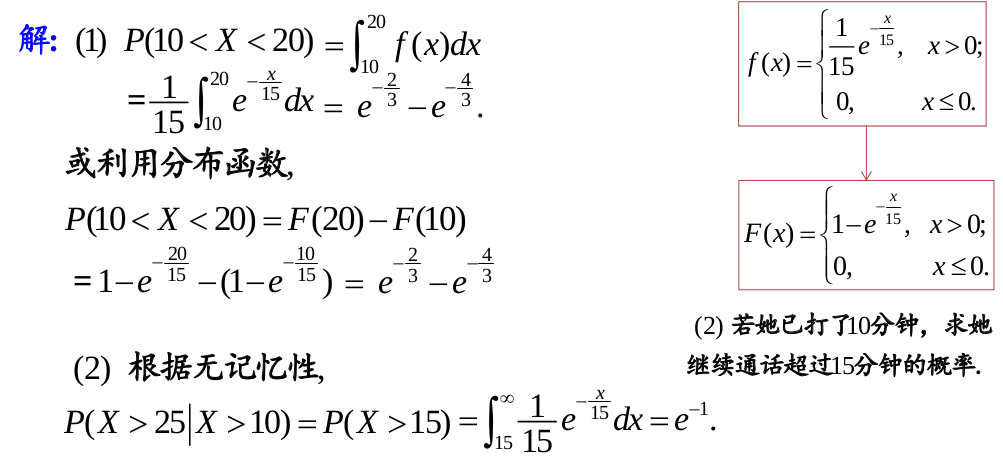
关于高斯分布的性质如下图:
自然界和人类社会中很多现象可以看做正态分布
如: 人的生理尺寸(身高、体重);
医学检验指标(红细胞数、血小板);
测量误差;等等
多个随机变量的和可以用正态分布来近似
如: 注册MOOC的某位同学完成所有作业的时间;
二项分布; 等等
(By 中心极限定理)
 本图描绘了多次抛掷硬币实验中出现正面的平均比率,每次实验均抛掷了大量硬币。
本图描绘了多次抛掷硬币实验中出现正面的平均比率,每次实验均抛掷了大量硬币。
而对于条件概率和联合概率的区别请看下面的例子:
//TODO待截图
(1)独立就是每次抽样之间是没有关系的,不会相互影响
就像我抛色子每次抛到几就是几这就是独立的
但若我要两次抛的和大于8,其余的不算,那么第一次抛和第二次抛就不独立了,因为第二次抛的时候结果是和第一次相关的
(2)同分布的意思就是每次抽样,样本都服从同样的一个分布
抛色子每次得到任意点数的概率都是1/6,这就是同分布的
但若我第一次抛一个六面的色子,第二次抛一个正12面体的色子,就不再是同分布了
(3)独立同分布,也叫i,i,d,就是每次抽样之间独立而且同分布的意思
追问:
同分布是指服从同一分布函数么?是的。
随机变量X和Y的联合分布函数是设(X,Y)是二维随机变量,对于任意实数x,y,二元函数:F(x,y) = P{(X<=x) 交 (Y<=y)} => P(X<=x, Y<=y)称为二维随机变量(X,Y)的分布函数。
* 关于二元的条件和边际分布,请查看慕课
* 注意边际分布和条件分布也是一个一元的高斯分布。
probability_math
先上一个例子:

答:

就是先给出一定的样本结果,通过结果来极大的估计参数值,需要注意的是,这里是知道分布而求参数(与EM算法要区别开),使得得到这样结果的可能性最大
如果是离散型的就是随机事件的概率,如果是连续型的可能就是一个参数具体看课件:极大似然估计
给出连续型和离散型的标准定义:


再举个例子:

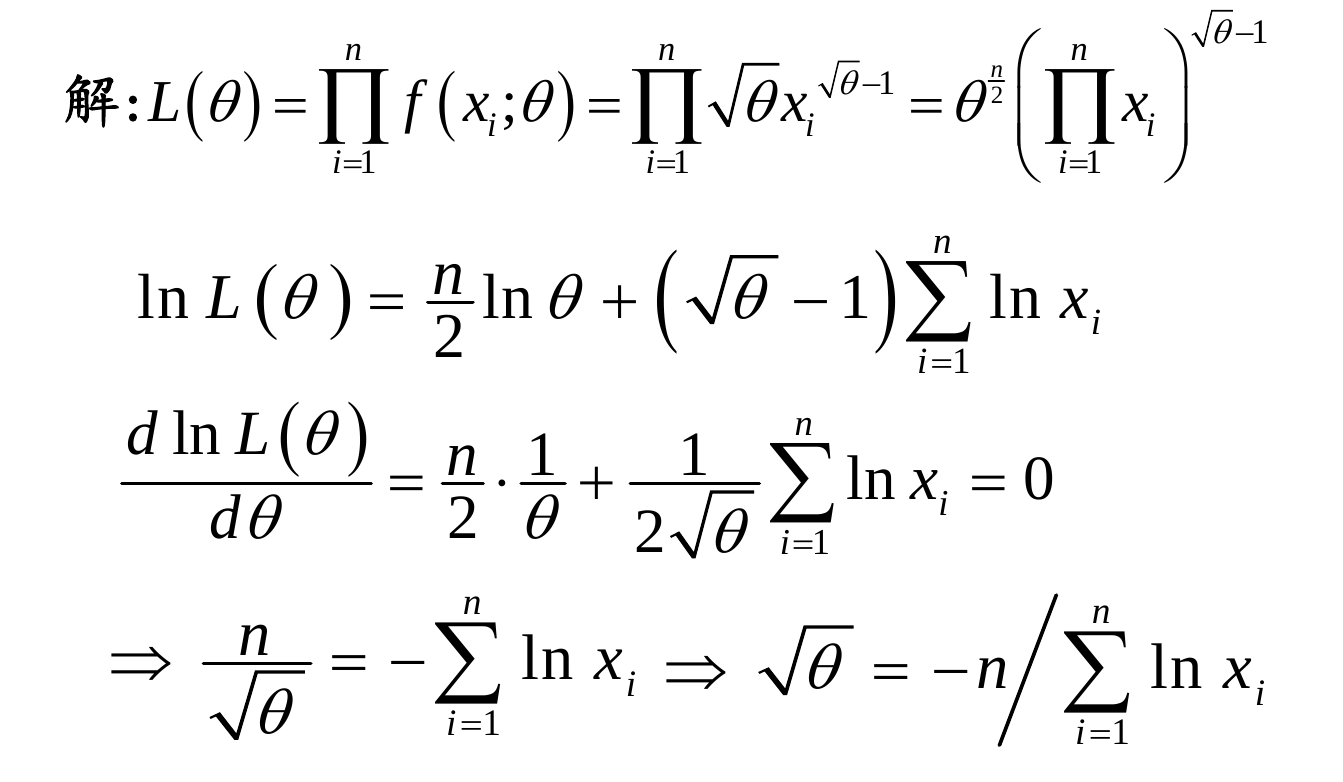
其实对L(θ)取对数将其变成连加的H(θ)还有一个原因:通常L(θ)中每个p(xi; θ)都很小,许多很小的数字相乘起来在计算机里很容易造成浮点数下溢,所以对其取对数将其变成连加的
讲到极大似然就想起EM算法,他们之间有很大的联系
EM算法是为了解决“最大似然估计”中更复杂的情形而存在的。 这里“极大似然估计中更复杂的情形”是什么情形呢? 我们知道极大似然估计是求解实现结果的最佳参数θ,但极大似然估计需要面临的概率分布只有一个或者知道结果是通过哪个概率分布实现的,只不过你不知道这个概率分布的参数。而如果概率分布有多个呢或者你不知道结果是通过哪个概率分布实现的?于是别说去确定“这些概率分布”的最佳参数了,我们连最终结果是根据哪个概率分布得出来的都不知道,这就是EM算法要面临的情况了。有关EM算法更多看我的那篇博文EM算法
参考资料:
《深度学习》-Bengio
《统计学习方法》-李航
《机器学习》-周志华
《机器学习实战》-Peter Harrington
斯坦福大学公开课-机器学习
网上的各位大牛的博文