

欢迎在文章下方评论,建议用电脑看
标准差和方差一般是用来描述一维数据的,但现实生活我们常常遇到含有多维数据的数据集,最简单的 大家上学时免不了要统计多个学科的考试成绩。面对这样的数据集,我们当然可以按照每一维独立的计算其方差,但是通常我们还想了解更多,比如,一个男孩子的 猥琐程度跟他受女孩子欢迎程度是否存在一些联系啊,嘿嘿~协方差就是这样一种用来度量两个随机变量关系的统计量
理解协方差矩阵的关键就在于牢记它计算的是不同维度之间的协方差,而不是不同样本之间,拿到一个样本矩阵,我们最先要明确的就是一行是一个样本还是一个维度,心中明确这个整个计算过程就会顺流而下,这么一来就不会迷茫了
举个例子:
问题: 有一组数据(如下),分别为二维向量,这四个数据对应的协方差矩阵是多少?
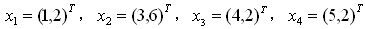
解答: 由于数据是二维的,所以协方差矩阵是一个22的矩阵,矩阵的每个元素为: 元素(i,j) = (第 i 维所有元素 - 第 i 维的均值) * (第 j 维所有元素 - 第 j 维的均值) 。 其中「」代表向量内积符号,即两个向量求内积,对应元素相乘之后再累加。 我们首先列出第一维:
D1: (1,3,4,5) 均值:3.25 D2: (2,6,2,2) 均值:3
下面计算协方差矩阵第(1,2)个元素:
元素(1,2)=(1-3.25,3-3.25,4-3.25,5-3.25)*(2-3,6-3,2-3,2-3)=-1
类似的,我们可以把全部个元素都计算出来:
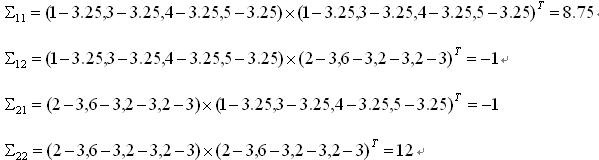
这个题目的最终结果就是:
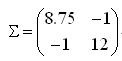
看完上面的例子,现在来总结以下它的特点:
协方差矩阵在二元高斯分布中决定了它的形状,详细演示
在降维技术那篇博文中,我们讲述了PCA,和这里的协方差矩阵有极大关系,在神经网络-基本概念中,讲述了数据预处理的白化,也是跟协方差矩阵有极大的关系。其实在机器学习中,很多时候,协方差矩阵都扮演着非常重要的角色,在这里就不一一的列出了,我们要好好的理解协方差矩阵的意义,关于它,给出一篇不错的博文
所有特征值都是正数的矩阵被称为正定;所有特征值都是非负数的矩阵被称为半正定。 同样地,所有特征值都是负数的矩阵被称为负定;所有特征值都是非正数的矩阵被称为半负定。 半正定矩阵受到关注是因为它们保证∀x,x⊤Ax≥0。 此外,正定矩阵还保证x^⊤Ax=0⇒x=0
我相信学过线性代数的小伙伴,一定对特征分解不陌生
许多数学对象可以通过将它们分解成多个组成部分,或者找到它们的一些属性而更好地理解,这些属性是通用的,而不是由我们选择表示它们的方式引起的。
例如:整数可以分解为质数。 我们可以用十进制或二进制等不同方式表示整数12,但质因数分解永远是对的12=2×3×3。 从这个表示中我们可以获得一些有用的信息,比如12不能被5整除,或者12的倍数可以被3整除。
正如我们可以通过分解质因数来发现整数的一些内在性质,我们也可以通过分解矩阵来发现矩阵表示成数组元素时不明显的函数性质。
特征向量的原始定义:
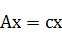
可以很容易看出,cx是方阵A对向量x进行变换后的结果,显然cx和x的方向相同。而且x是特征向量的话,ax也是特征向量(a是标量且不为零),所以特征向量不是一个向量而是一个向量族。
另外,特征值只不过反映了特征向量在变换时的伸缩倍数而已。对一个变换而言,特征向量指明的方向才是很重要的,特征值不那么重要。虽然我们求这两个量时先求出特征值,但特征向量才是更本质的东西!特征向量是指经过指定变换(与特定矩阵相乘)后不发生方向改变的那些向量,特征值是指在经过这些变换后特征向量的伸缩的倍数,也就是说矩阵对某一个向量或某些向量只发生伸缩变换,不对这些向量产生旋转的效果,那么这些向量就称为这个矩阵的特征向量,伸缩的比例就是特征值。
实际上,上述的一段话既讲了矩阵变换特征值及特征向量的几何意义(图形变换)也讲了其物理含义。物理的含义就是运动的图景:特征向量在一个矩阵的作用下作伸缩运动,伸缩的幅度由特征值确定。特征值大于1,所有属于此特征值的特征向量身形暴长;特征值大于0小于1,特征向量身形猛缩;特征值小于0,特征向量缩过了界,反方向到0点那边去了。
注意:常有教科书说特征向量是在矩阵变换下不改变方向的向量,实际上当特征值小于零时,矩阵就会把特征向量完全反方向改变,当然特征向量还是特征向量。我赞同特征向量不改变方向的说法:特征向量永远不改变方向,改变的只是特征值(方向反转特征值为负值了)。特征向量是线性不变量
特征向量和特征值可以直接应用于机器学习中,如PCA,下面有个简单的例子
机器学习中的分类问题,给出178个葡萄酒样本,每个样本含有13个参数,比如酒精度、酸度、镁含量等,这些样本属于3个不同种类的葡萄酒。任务是提取3种葡萄酒的特征,以便下一次给出一个新的葡萄酒样本的时候,能根据已有数据判断出新样本是哪一种葡萄酒。
原数据有13维,但这之中含有冗余,减少数据量最直接的方法就是降维。做法:把数据集赋给一个178行13列的矩阵R,减掉均值并归一化,它的协方差矩阵C是13行13列的矩阵,对C进行特征分解,对角化
,其中U是特征向量组成的矩阵D是特征之组成的对角矩阵,并按由大到小排列。然后,另R’ =RU,就实现了数据集在特征向量这组正交基上的投影。嗯,重点来了,R’中的数据列是按照对应特征值的大小排列的,后面的列对应小特征值,去掉以后对整个数据集的影响比较小。比如,现在我们直接去掉后面的7列,只保留前6列,就完成了降维。这个降维方法叫PCA(Principal Component Analysis)。降维以后分类错误率与不降维的方法相差无几,但需要处理的数据量减小了一半(不降维需要处理13维,降维后只需要处理6维)。这显示了PCA的威力
奇异值分解和上面所讲的特征分解有很大的关系,而我的理解是:
奇异值分解的含义是,把一个矩阵A看成线性变换(当然也可以看成是数据矩阵或者样本矩阵),那么这个线性变换的作用效果是这样的,我们可以在原空间找到一组标准正交基V,同时可以在像空间找到一组标准正交基U,我们知道,看一个矩阵的作用效果只要看它在一组基上的作用效果即可,在内积空间上,我们更希望看到它在一组标准正交基上的作用效果。而矩阵A在标准正交基V上的作用效果恰好可以表示为在U的对应方向上只进行纯粹的伸缩!这就大大简化了我们对矩阵作用的认识,因为我们知道,我们面前不管是多么复杂的矩阵,它在某组 标准正交基上的作用就是在另外一组标准正交基上进行伸缩而已。
更加详细的讲述请看:奇异值的意义
特征分解也是这样的,也可以简化我们对矩阵的认识。对于可对角化的矩阵,该线性变换的作用就是将某些方向(特征向量方向)在该方向上做伸缩。
有了上述认识,当我们要看该矩阵对任一向量x的作用效果的时候,在特征分解的视角下,我们可以把x往特征向量方向上分解,然后每个方向上做伸缩,最后再把结果加起来即可;在奇异值分解的视角下,我们可以把x往V方向上分解,然后将各个分量分别对应到U方向上做伸缩,最后把各个分量上的结果加起来即可。
参考资料:
《深度学习》-Bengio
《统计学习方法》-李航
《机器学习》-周志华
《机器学习实战》-Peter Harrington
斯坦福大学公开课-机器学习
网上的各位大牛的博文