欢迎在文章下方评论，建议用电脑看
一句话概述Adaboost算法的话就是：把多个简单的分类器结合起来形成个复杂的分类器。也就是“三个臭皮匠顶一个诸葛亮”的道理。
下面先来一个简单的认识：
如下图所示： 在D1这个数据集中有两类数据“+”和“-”。
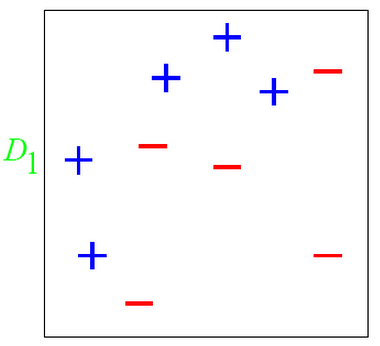
对于这个数据集，你会发现，用简单分类器，不管是这么分，都无法很好的分类
我们这样分：
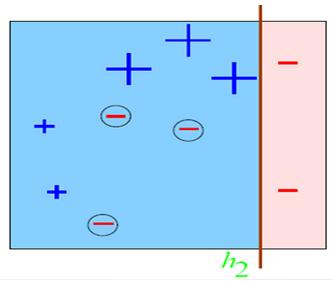
或者这样分：
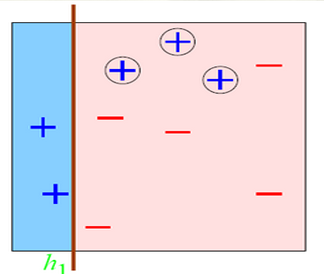
总有误分类点存在； 那么如果我们把上面三种分发集合起来呢？像下面这样：
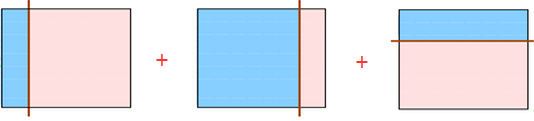
会发现把上面三个弱分类器组合起来会变成下面这个分类器：
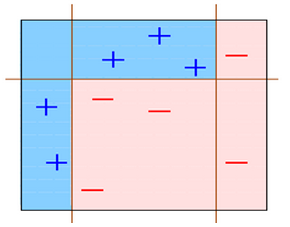
这样一来用这个分类器就可以完美的分类数据了。 可以说这就是集成学习的整体思想！
是不是十分简单粗暴？好了，下面我们就正经的说下集成学习：
既然集成学习分为Boosting，Bagging和RF。那下面我们就从这些分类中讲，在这篇博文中，我会讲下Boosting的代表：AdaBoost和提升树，讲下Bagging的代表：随机森林。
Adaboost的巧妙之处就在于它将这些想法自然且有效地实现在一种算法里。
然后对上面的步骤做一些说明：
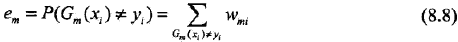
这里，wmi表示第m轮中第i个实例的权值，且：
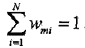
这表明，Gm(x)在加权的训练数据集上的分类误差率是被Gm(x)误分类样本的权值之和，由此可以看出数据权值分布Dm与弱分类器Gm(x)的分类误差率的关系。 c: 计算弱分类器Gm(x)的系数am，am表示Gm(x)在最终分类器中的重要性。由式8.2可知，当em <= 1/2时，am >=0，并且am随em的减小而增大，所以分类误差率越小的弱分类器在最终分类器中的作用越大。 d: 更新训练数据的权值分布为下一轮做准备。式8.4可以写成：
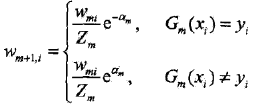
由此可知，被弱分类器Gm(x)误分类样本的权值得以扩大，而被正确分类样本的权值却得以缩小。两相比较，误分类样本的权值被放大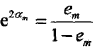
倍。
因此，误分类样本在下一轮学习中起更大的作用。
而，“不改变所给的训练数据，而不断改变训练数据的权值分布，使得训练数据在若分类器的学习中起不同的作用”就是Adaboost的一个特点。
步骤3中通过线性组合f(x)实现M个弱分类器的加权表决。系数am表示了弱分类器Gm(x)的重要性，这里，所有am之和并不为1。f(x)的符号决定实例x的类，f(x)的绝对值表示分类的确信度。“利用弱分类器的线性组合构建最终分类器”是Adaboost的另一个特点。
讲完上面的基本概念，我们直接上《统计学习方法》的例子：
给定上面这张训练数据表所示的数据，假设弱分类器由x<v或x>v产生，其阈值v使该分类器在训练数据集上的分类误差率最低，试用Adaboost算法学习一个强分类器。
解：
1. 令m = 1
则初始化数据权值分布：
Dm = (wm1, wm2,..., wm10)，即：D1 = (w11, w12, ..., w110)
wmi = 0.1， i = 1, 2,..., 10，即：w1i = 0.1， i = 1, 2, ..., 10
a:用下面的方式从v=1.5遍历到v=9.5
for( v=1.5;v<=9.5; v++) {
if(x < v) G1(x)=1;
elseif (x > v) G1(x) = -1;
}
并统计v取各个值使得误差率(误差率的计算方法是：所有误分类点的权值之和)。
然后发现，当v取2.5时，误分类点为x=6, 7, 8，其权值和为0.3，误差率最低，此时，当前弱分类器为：
G1(x) 在训练数据集上的误差率e1= P(G1(xi) != yi) = 0.3
b:计算G1(x)的系数：a1 =(1/2) log [(1-e1)/e1] = 0.4236
c:更新训练数据的权值分布：
D2= (w21, w22, ...,w210)
w2i= (w1i/Z1)exp(-a1yiG1(xi))，i = 1, 2,..., 10
于是
D2 = (0.0715, 0.0715, 0.0715, 0.0715,0.0715, 0.0715, 0.1666, 0.1666, 0.1666, 0.0715)
f1(x) = 0.4236G1(x)
分类器sign[f1(x)]在训练数据集上有3个误分类点。
2. 令m = 2，做和上一步同上的操作。
发现在权值分布为D2的训练数据上，v = 8.5时误差率最低，此时：
当前弱分类器为：
误差率是e2 = 0.2143
a2= 0.6496
于是
权值分布为：D3 =(0.0455, 0.0455, 0.0455, 0.1667, 0.1667, 0.1667, 0.1060, 0.1060, 0.1060,0.0455)
f2(x)= 0.4236G1(x) + 0.6496G2(x)
分类器sign[f2(x)]在训练数据集上有3个误分类点。
3. 令m = 3。
所以在权值分布为D3的训练数据上，v =5.5时分类误差率最低，此时的弱分类器为：
G3(x)在训练样本上的误差率为e3= 0.1820
a3= 0.7514
于是
权值分布为：D4 =(0.125, 0.125, 0.125, 0.102, 0.102, 0.102, 0.065, 0.065, 0.065, 0.125)
f3(x)= 0.4236G1(x) + 0.6496G2(x) + 0.7514G3(x)
因为分类器sign[f3(x)]在训练数据集上的误分类点个数为0.
于是最终分类器为：
G(x)= sign[f3(x)] = sign[0.4236G1(x) + 0.6496G2(x)+ 0.7514G3(x)]
可以说，通过这个例子，我们教好的理解了Adaboost的大致思想。
AdaBoost算法还有另一个解释，即可以认为AdaBoost算法是模型为加法模型、损失函数为指数函数、学习算法为前向分步算法时的二类分类学习方法。 前向分步算法(forward stagewise algorithm)
加法模型：
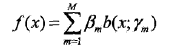
其中，b为基函数，r为基函数的参数，beta为基函数的系数。 前向分步算法同时求解从m=1到M所有参数的优化问题简化为逐次求解各个参数的优化问题.
注意：前向分步算法与AdaBoost是等价的。
提升树是以分类树或回归树为基本分类器的提升方法。提升树被认为是统计学习中性能最好的方法之一。
提升方法实际采用加法模型(即基函数的线性组合)与前向分步算法。以决策树为基函数的提升方法称为提升树(boosting tree)。对分类问题决策树是二叉分类树，对回归问题决策树是二叉回归树。
基本分类器x<v或x>v，可以看作是由一个根结点直接连接两个叶结点的简单决策树，即所谓的决策树桩(decision stump)。
提升树模型可以表示为决策树的加法模型:
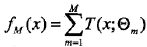
其中，T表示决策树，theta为决策树的参数，M为树的个数。
提升树算法采用前向分步算法。首先确定初始提升树f0(x)=0，第m步的模型是
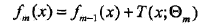
其中，fm-1(x)为当前模型，通过经验风险极小化确定下一棵决策树的参数。
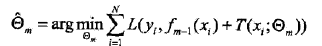
不同问题的提升树学习算法主要区别在于使用的损失函数不同。包括用平方误差损失函数的回归问题，用指数损失函数的分类问题，以及用一般损失函数的一般决策问题。 对于二类分类问题，提升树算法只需将AdaBoost算法8.1中的基本分类器限制为二类分类树即可，是AdaBoost算法的特殊情况。
当采用平方误差损失函数时，
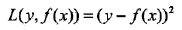
在前向分步算法的第m步，损失变为，
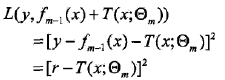
其中是当前模型拟合数据的残差(residual)。 所以对回归问题的提升树算法来说，求解经验风险极小化的问题只需简单地拟合当前模型的残差。
梯度提升算法（GBDT）
提升树利用加法模型与前向分步算法实现学习的优化过程。当损失函数是平方损失和指数损失函数时。每一步优化是很简单的。但对一般损失函数而言，往往每一步优化并不那么容易。针对这一问题，Freidmao提出了梯度提升(gradient boosting)算法。这是利用最速下降法的近似方法，其关键是利用损失函数的负梯度在当前模型的值:
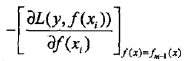
作为回归问题提升树算法中的残差的近似值，拟合一个回归树。
算法第1步初始化，估计使损失函数极小化的常数值，它是只有一个根结点的树，即 x>c 和 x<c；
第2 (a)步计算损失函数的负梯度在当前模型的值，将它作为残差的估计。对于平方损失函数，它就是通常所说的残差；对 于一般损失函数，它就是残差的近似值。
第2 (b)步估计回归树叶结点区域，以拟合残差的近似值
第2 (c)步利用线性搜索估计叶结点区域的值，使损失函数极小化
第2 (d)步更新回归树。
第3步得到输出的最终模型。
还是《统计学习方法》的那个例子，直接上截图（逃）：
xgboost是在GBDT的基础上对boosting算法进行的改进，内部决策树使用的是回归树,它和GBDT大体类似就不细讲了，但XGBoost风靡Kaggle、天池、DataCastle、Kesci等国内外数据竞赛平台，是比赛夺冠的必备大杀器。所以还是挺常用的，所以这里说下：
xgboost相比传统gbdt有何不同？xgboost为什么快？xgboost如何支持并行？
xgboost使用经验总结
需要注意的是Boosting算法在训练的每一轮都要检查当前生成的基学习器是否满足基本条件（检查基分类器是否比随机猜测好），一旦条件不满足，当前基学习器被抛弃掉，学习过程停止。在这种情形下，初始设置的学习轮数T也许还远远未达到，可能导致最终集成中只包含很少的基学习器而导致性能不佳。若采用“重采样”，则可以获得“重启动”机会避免过早停止。即在抛弃不满足条件的当前基学习器之后，根据当前的分布重新对训练样本进行采样，再基于新的采样结果重新训练出基学习器，从而使得学习过程可以持续到预制的T轮。
从“偏差-方差”分解的角度看，Boosting主要关注降低偏差，因此基于泛化性能相当弱学习器能构建出很强的集成。
参考资料：
《统计学习方法》-李航
《机器学习》-周志华
《机器学习实战》-Peter Harrington
斯坦福大学公开课-机器学习
网上的各位大牛的博文
