

欢迎在文章下方评论,建议用电脑看
上一篇博文我们讲了Boosting,这篇博文我们接着讲Bagging,主要讲解随机森林算法,通过这个算法来了解Bagging。
Bagging是“并行式”集成学习方法中最著名的代表,基于我们之前介绍的自主采样法。给定包含m个样本的数据集,随机取出一个样本放入采样机,再将样本放回初始数据集,使得下次采样仍有可能被选中,经过m次随机采样,得到m个样本的数据集,初始数据集中约63.2%出现在采样集中。注意:有放回的抽样
我们采样出T个含m个训练样本的采样集,然后基于每个采样集训练出一个基学习器,再将这些基学习器进行结合。
在对预测输出进行结合的时候,Bagging通常对分类任务采用简单投票法,回归任务采用简单平均法,若遇到相同票数则随机选择一个或者根据投票置信度来选择。
训练一个Bagging集成与直接使用基学习算法训练一个学习器复杂度同阶,说明是一个高效的集成算法,与标准AdaBoost只适用于二分类任务不同,Bagging可以不经修改的用于多分类、回归等任务。
随机森林,指的是利用多棵树对样本进行训练并预测的一种分类器。该分类器最早由Leo Breiman和Adele Cutler提出,并被注册成了商标。简单来说,随机森林就是由多棵CART(Classification And Regression Tree)构成的。对于每棵树,它们使用的训练集是从总的训练集中有放回采样出来的,这意味着,总的训练集中的有些样本可能多次出现在一棵树的训练集中,也可能从未出现在一棵树的训练集中。在训练每棵树的节点时,使用的特征是从所有特征中按照一定比例随机地无放回的抽取的,根据Leo Breiman的建议,假设总的特征数量为M,这个比例可以是sqrt(M),1/2sqrt(M),2sqrt(M)。
随机森林是Bagging的一个扩展变体。RF在以决策树为基学习器,构建Bagging的基础上,进一步在决策树的训练过程中引入了随机属性选择。
具体来说,传统的决策树在选择划分属性的时候是在当前节点的属性集合中选择一个最优属性,而在RF中,对基决策树的每个节点,先从该节点的属性集中随机选择一个包含k个属性的子集,然后再从这个子集中选择一个最优属性用于划分。
这里的参数k控制了随机性的引入程度,若令k=d,则基决策树的构建与传统决策树相同;
若k=1,则随机选择一个属性进行划分;一般情况下推荐k=log_2 d
随机森林简单,容易实现,计算开销小,令人惊奇的是,在很多现实任务中展现出强大的性能,誉为“代表集成学习技术水平的方法”。
可以看出,随机森林对Bagging只做了微小的改动,但是与Bagging中基学习器的“多样性”仅通过样本扰动(通过对初始训练集采样)而来不同,随机森林中基学习器的多样性不仅来自于样本扰动,还来自于属性扰动,这就使得最终集成的泛化性能可以通过个体学习器之间的差异度的增加而进一步提升。
随机森林的收敛性与bagging相似,随机森林其实性能很差,随着个体学习器增加,会收敛到更低泛化性能。
随机森林训练效率通常优于bagging,因为在个体决策树的构建过程中,bagging使用的是“确定型”决策树,需要考虑全部属性,但是随机森林使用的是“随机型”只需要考虑一个属性集合。
** 利用随机森林的训练过程如下:**
对于第1-t棵树,i=1-t:
从S中有放回的抽取大小和S一样的训练集S(i),作为根节点的样本,从根节点开始训练
如果当前节点上达到终止条件,则设置当前节点为叶子节点,如果是分类问题,该叶子节点的预测输出为当前节点样本集合中数量最多的那一类c(j),概率p为c(j)占当前样本集的比例;如果是回归问题,预测输出为当前节点样本集各个样本值的平均值。然后继续训练其他节点。如果当前节点没有达到终止条件,则从F维特征中无放回的随机选取f维特征。利用这f维特征,寻找分类效果最好的一维特征k及其阈值th,当前节点上样本第k维特征小于th的样本被划分到左节点,其余的被划分到右节点。继续训练其他节点。有关分类效果的评判标准在后面会讲。
重复(2)(3)直到所有节点都训练过了或者被标记为叶子节点。
重复(2),(3),(4)直到所有CART都被训练过。
** 利用随机森林的预测过程如下:**
对于第1-t棵树,i=1-t:
(1)从当前树的根节点开始,根据当前节点的阈值th,判断是进入左节点(<th)还是进入右节点(>=th),直到到达,某个叶子节点,并输出预测值。
(2)重复执行(1)直到所有t棵树都输出了预测值。如果是分类问题,则输出为所有树中预测概率总和最大的那一个类,即对每个c(j)的p进行累计;如果是回归问题,则输出为所有树的输出的平均值。
注意:这里讲的是随机森林的原理,而不是真正就这样生成的。
描述:根据已有的训练集已经生成了对应的随机森林,随机森林如何利用某一个人的年龄(Age)、性别(Gender)、教育情况(Highest Educational Qualification)、工作领域(Industry)以及住宅地(Residence)共5个字段来预测他的收入层次。
收入层次 :
Band 1 : Below $40,000
Band 2: $40,000 – 150,000
Band 3: More than $150,000
随机森林中每一棵树都可以看做是一棵CART(分类回归树),这里假设森林中有5棵CART树,总特征个数N=5,我们取m=1(这里假设每个CART树对应一个不同的特征)。
CART 1 : Variable Age
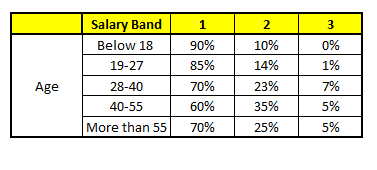
CART 2 : Variable Gender
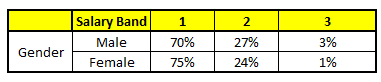
CART 3 : Variable Education
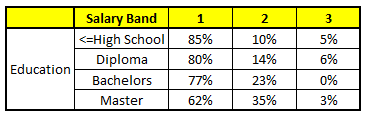
CART 4 : Variable Residence

CART 5 : Variable Industry
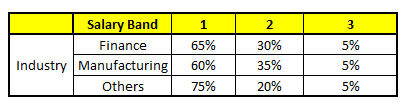
我们要预测的某个人的信息如下:
1. Age : 35 years ; 2. Gender : Male ; 3. Highest Educational Qualification : Diploma holder; 4. Industry : Manufacturing; 5. Residence : Metro.
根据这五棵CART树的分类结果,我们可以针对这个人的信息建立收入层次的分布情况:
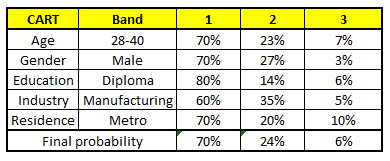
最后,我们得出结论,这个人的收入层次70%是一等,大约24%为二等,6%为三等,所以最终认定该人属于一等收入层次(小于$40,000)。
随机森林的最佳使用实例之一是特征选择(feature selection)。尝试许多决策树变量(variations)带来的副产品之一是,你可以检验每棵树中哪个变量最相关/无关。
随机森林也很擅长分类任务。它能用于对具有多个可能值的类别进行预测,也能被校准来输出概率。需要注意的是过拟合(overfitting)。随机森林可能容易过拟合,尤其是使用相对小型的数据集时。如果你的模型在我们的测试集中表现“太好”,就应该怀疑过拟合了。
我发现随机森林——不像其他算法——在学习分类变量或分类变量和真实变量的结合时真的很有效。高基数的分类变量处理起来很棘手,因此随机森林会大有帮助。
在数据集上表现良好
在当前的很多数据集上,相对其他算法有着很大的优势
它能够处理很高维度(feature很多)的数据,并且不用做特征选择
在训练完后,它能够给出哪些feature比较重要
在创建随机森林的时候,对generlization error使用的是无偏估计
训练速度快
在训练过程中,能够检测到feature间的互相影响
容易做成并行化方法
实现比较简单
随机森林比较简单,下面就再用网上的(Python实现)例子来结束对它的讲解:
参考资料:
《统计学习方法》-李航
《机器学习》-周志华
《机器学习实战》-Peter Harrington
斯坦福大学公开课-机器学习
网上的各位大牛的博文