目录

欢迎在文章下方评论，建议用电脑看

• 目录
• 机器学习基础概念
  • 过拟合和欠拟合
  • 偏差/方差权衡
  • 模型复杂程度和偏差/方差权衡
  • What is the difference between (bias variance) and (underfitting overfitting)?
  • 正则化
  • 误差验证-评估方法
    • KL散度

机器学习基础概念

过拟合和欠拟合

过拟合（overfitting）：学习能力过强，以至于把训练样本所包含的不太一般的特性都学到了。 欠拟合（underfitting）：学习能太差，训练样本的一般性质尚未学好。

在周志华教授的《机器学习》中有个比较的类比：

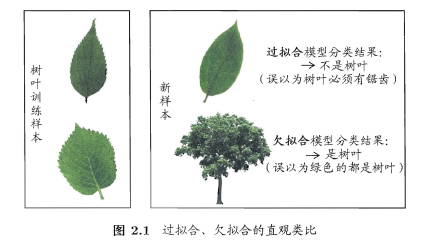
下面在那一个真实的例子： 如果我们有6个数据，我们选择用怎么样的回归曲线对它拟合呢？看下图

1. 可以发现得到的直线y=b+a*x 并不能较为准确的描述训练数据的形态，我们说这不是一个良好的拟合。这也叫做欠拟合
2. 如果我们再加入一个特征值 x^2，得到y=a+b*x+c *x^2于是我们得到一个稍好的拟合
3. 最后我们直接用五阶多项式去拟合，发现对于训练样本可以很好的拟合，但是这样的模型对预测往往效果不是非常好，这叫做过拟合（overfitting）。

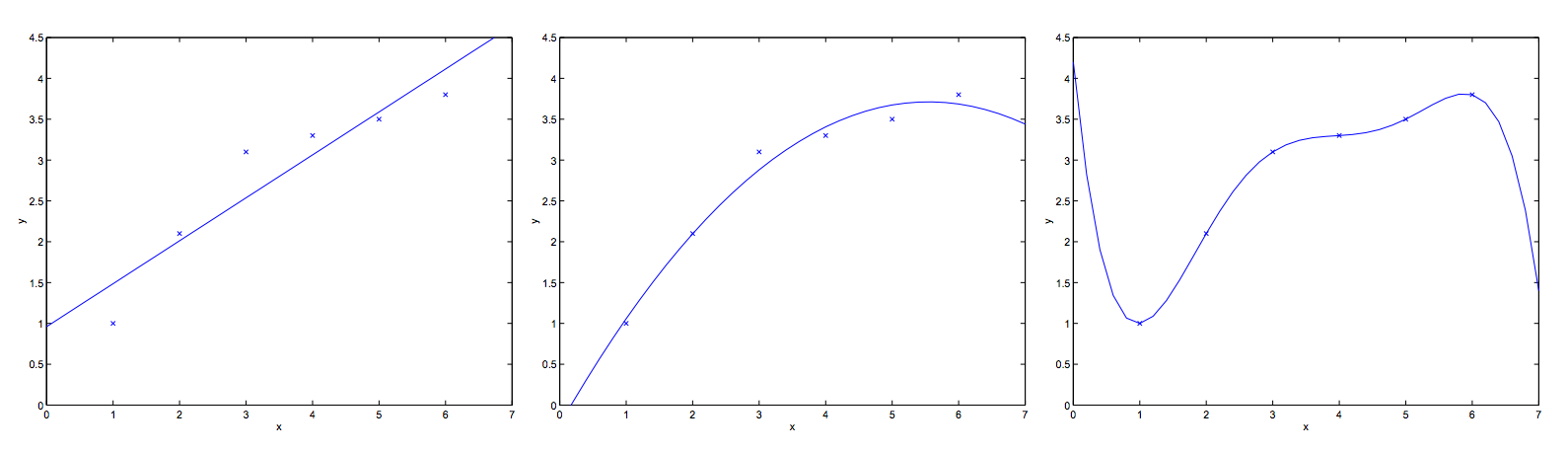
在这里我们可以发现，原来过拟合和欠拟合和模型复杂度是相关的，具体描述如下图

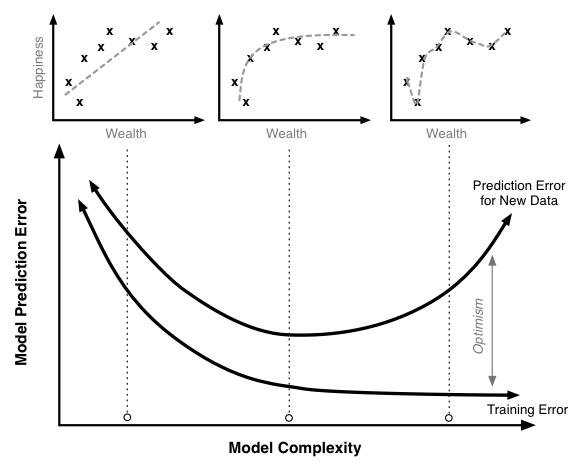
好了，应该了解什么叫欠拟合和过拟合了吧！

当然，为了防止过拟合，也会有cross validation，正则化，dropout等等方法，以后会一一介绍。

偏差/方差权衡

　　偏差-方差分解是解释学习器泛化性能的重要工具。在学习算法中，偏差指的是预测的期望值与真实值的偏差，方差则是每一次预测值与预测值得期望之间的差均方，当然还有任务本身的噪音。实际上，偏差体现了学习器预测的准确度，而方差体现了学习器预测的稳定性。噪声表达当前任务在任何学习算法所能达到的泛化误差的下界，通过对泛化误差的进行分解。可以得到：

• 期望泛化误差=方差+偏差+噪声
• 偏差刻画学习器的拟合能力
• 方差体现学习器的稳定性
• 噪音刻画了问题本身的难度

方差和偏差具有矛盾性，这就是常说的偏差-方差窘伪境（bias-variance dilamma），随着训练程度的提升，期望预测值与真实值之间的差异越来越小，即偏差越来越小，但是另一方面，随着训练程度加大，学习算法对数据集的波动越来越敏感，方差值越来越大。换句话说：在欠拟合时，偏差主导泛化误差，而训练到一定程度后，偏差越来越小，方差主导了泛化误差。因此训练也不要贪杯，适度辄止。

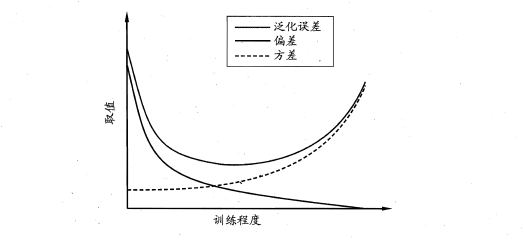（最上面的线是泛化误差）

模型复杂程度和偏差/方差权衡

我们在偏差与方差间都会做出权衡。如果我们的模型过于简单，只有很少的几个参数，那么它可能存在着较大的偏差（但是方差较小）；如果过于复杂而含有非常多的参数，那么模型可能会存在较大的方差（但是偏差较小）

What is the difference between (bias variance) and (underfitting overfitting)?

参考文章

All are metrics to find the best model: You would like to have an unbiased minimum variance estimator related to the validation interval - and thus neither over nor underfitted. But how to balance these metrics is up to your application / context.

Bias: The error you have for certain even if you can use an infinite number of cases / records. Usually you try to get unbiased models.

Variance / Significance: Relates to the probability that the true relationships between your variables are trivial (e.g. zero) and your model sees an accidental and purely randomly generated data pattern. Variance and bias are usually independent.

Overfitting: Is related to the variance, but it’s not the same. If you have a large data matrix you may fit a model with a large number of covariats and many parameters may have a small variance. Nevertheless if you split off 20% of the training material and make a prediction with your model on that validation data, the model may predict worse. That’s overfitting: Your model fitted relationships, which aren’t randomly within your full data set, but aren’t systematic and stable 伪for extrapolations outside the training data set.

Underfitting goes usually with a biased distribution of your residuals: Your model is insufficiently specified. (Relationship between target and covariat is quadratic, but you fit linear). Underfitting can result in a bias, but doesn’t have to do. In any case it results in a non-minimal variance.

一般而言高偏差意味着欠拟合，高方差意味着过拟合,但是他们并不是直接相等

正则化

书上说正则化是模型选择的一种方式，但其实我更赞同它的直接目的是防止过拟合！不过我们做的一切都是为了建立选出一个更好的模型是吧！

1. 正则化的目的：防止过拟合！
2. 正则化的本质：约束（限制）要优化的参数。
3. 正则化实现方式：在Cost function误差函数中添加惩罚项
4. 正则化的缺点：正则化防止过拟合，但引入正则化可能会引起“too much regularization”

问：对于正则化，优点是使模型“简单”–》这”简单”怎么理解？ 答：引用李航老师书中的那段话：正则化符合奥卡姆剃刀 (Occam’s razor)原理。奥卡姆剃刀原理应用于模型选择时变为以下想法：在所有可能选择的模型中，能够很好地解释已知数据并且十分简单才是最好的模型，也就是应 该选择的模型。从贝叶斯估计的角度来看，正则化项对应于模型的先验概率。可以假设复杂的模型有较大的先验概率，简单的模型有较小的先验概率。

还是通过例子来描述和理解：下面选自斯坦福大学机器学习公开课 下面是对房子的面积特征和价格的拟合

1. 合适的拟合：

1. 过拟合：

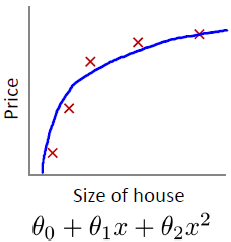
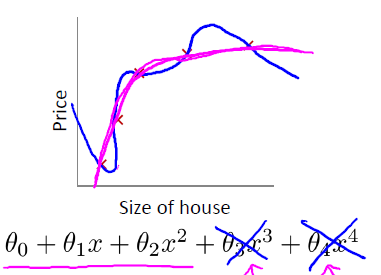
直观来看，如果我们想解决这个例子中的过拟合问题，最好能将x3,x4的影响消除，也就是让θ3≈0,θ4≈0. 假设我们对θ3,θ4进行惩罚，并且令其很小，一个简单的办法就是给原有的Cost function()加上两个略大惩罚项，例如：

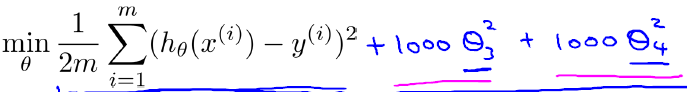
这样在最小化Cost function的时候，θ3≈0,θ4≈0.

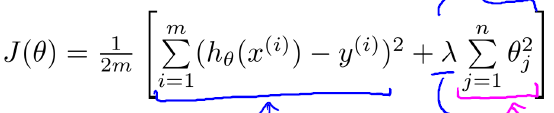
为了使正则化运作良好，我们应当注意一些方面，应该去选择一个不错的正则化参数 λ 。当我们以后讲到多重选择时我们将讨论一种方法来自动选择正则化参数 λ，为了使用正则化，那么我们就可以让他们避免过度拟合了。

误差验证-评估方法

最后说下误差验证评估方法，主要包括以下3种

• 保留交叉验证，也叫作留出法
  1. 从全部的训练数据 S中随机选择 中随机选择 s的样例作为训练集 train，剩余的 作为测试集 作为测试集 test。
  2. 通过对测试集训练 ，得到假设函数或者模型 。
  3. 在测试集对每一个样本根据假设函数或者模型，得到训练集的类标，求出分类正确率。
  4. 选择具有最大分类率的模型或者假设
• k折交叉验证 k-fold cross validation
  1. 将全部训练集 S分成 k个不相交的子集，假设 S中的训练样例个数为 m，那么每一个子 集有 m/k 个训练样例，相应的子集称作 {s1,s2,…,sk}。
  2. 每次从分好的子集中里面，拿出一个作为测试集，其它k-1个作为训练集
  3. 根据训练训练出模型或者假设函数。
  4. 把这个模型放到测试集上，得到分类率。
  5. 计算k次求得的分类率的平均值，作为该模型或者假设函数的真实分类率。 这个方法充分利用了所有样本。但计算比较繁琐，需要训练k次，测试k次。

当然，交叉验证中有一个比较特殊的情况—-留一法 留一法就是每次只留下一个样本做测试集（也就是当上面的k==m的情况），其它样本做训练集，如果有k个样本，则需要训练k次，测试k次。留一发计算最繁琐，但样本利用率最高。适合于小样本的情况。

我们希望评估的是用整个数据集S训练出的模型。但在留出法和交叉验证法中，由于保留了一部分样本用于测试，因此实际评估的模型所使用的训练集比S小，这必然会引入一些因训 练样本规模不同而导致的估计偏差。留一法受训练样本规模变化的影响较小，但计算复杂度又太高了。 这就引出下面的自助法

• 自助法
  1. 自助法的基本思想是：给定包含m个样本的数据集S，每次随机从S 中挑选一个样本，将其拷贝放入S’，然后再将该样本放回初始数据集S 中，使得该样本在下次采样时仍有可能被采到。
  2. 重复执行m 次，就可以得到了包含m个样本的数据集S’。可以得知在m次采样中，样本始终不被采到的概率取极限为：

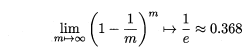
这样，通过自助采样，初始样本集S中大约有36.8%的样本没有出现在S’中，于是可以将S’作为训练集，S-S’作为测试集。自助法在数据集较小，难以有效划分训练集/测试集时很有用，但由于自助法产生的数据集（随机抽样）改变了初始数据集的分布，因此引入n了估计偏差。在初始数据集足够时，留出法和交叉验证法更加常用，我也是最常用交叉验证的。

KL散度

相对熵（relative entropy）又称为KL散度（Kullback–Leibler divergence，简称KLD），信息散度（information divergence），信息增益（information gain）。 KL散度是两个概率分布P和Q差别的非对称性的度量。

KL散度是用来度量使用基于Q的编码来编码来自P的样本平均所需的额外的比特个数。 典型情况下，P表示数据的真实分布，Q表示数据的理论分布，模型分布，或P的近似分布。

根据shannon的信息论，给定一个字符集的概率分布，我们可以设计一种编码，使得表示该字符集组成的字符串平均需要的比特数最少。假设这个字符集是X，对x∈X，其出现概率为P(x)，那么其最优编码平均需要的比特数等于这个字符集的熵：

H(X)=∑x∈XP(x)log[1/P(x)]

在同样的字符集上，假设存在另一个概率分布Q(X)。如果用概率分布P(X)的最优编码（即字符x的编码长度等于log[1/P(x)]），来为符合分布Q(X)的字符编码，那么表示这些字符就会比理想情况多用一些比特数。KL-divergence就是用来衡量这种情况下平均每个字符多用的比特数，因此可以用来衡量两个分布的距离。即：

DKL(Q||P)=∑x∈XQ(x)[log(1/P(x))] - ∑x∈XQ(x)[log[1/Q(x)]]=∑x∈XQ(x)log[Q(x)/P(x)]

由于-log(u)是凸函数，因此有下面的不等式

DKL(Q||P) = -∑x∈XQ(x)log[P(x)/Q(x)] = E[-logP(x)/Q(x)] ≥ -logE[P(x)/Q(x)] = -　　log∑x∈XQ(x)P(x)/Q(x) = 0

即KL-divergence始终是大于等于0的。当且仅当两分布相同时，KL-divergence等于0。

===========================

举一个实际的例子吧：比如有四个类别，一个方法A得到四个类别的概率分别是0.1,0.2,0.3,0.4。另一种方法B（或者说是事实情况）是得到四个类别的概率分别是0.4,0.3,0.2,0.1,那么这两个分布的KL-Distance(A,B)=0.1*log(0.1/0.4)+0.2*log(0.2/0.3)+0.3*log(0.3/0.2)+0.4*log(0.4/0.1)

这个里面有正的，有负的，可以证明KL-Distance()>=0.

从上面可以看出， KL散度是不对称的。即KL-Distance(A,B)!=KL-Distance(B,A)

KL散度是不对称的，当然，如果希望把它变对称，

Ds(p1, p2) = [D(p1, p2) + D(p2, p1)] / 2.

Donate

×Close

Donate Me

Thanks for your support!

• Alipay
• Wechat

Close

Share: